链表反转
Harshit Jindal
2024年2月15日
链表是线性数据结构。链表的一个节点包括:
- 数据项。
- 下一个节点的地址。
class Node {
int data;
Node *next;
};
本文将介绍如何在给定指向链表头节点的指针的情况下反转链表。
链表反转算法
令 head 成为链接列表的第一个节点。
迭代算法
-
初始化 3 个指针-
curr设置为head,prev和next设置为NULL。 -
遍历链接列表,直到到达最后一个节点,即
curr!=NULL并执行以下操作:- 将
next设置为curr->next 个,以将next移动到其下一个节点。 - 通过将当前节点指向
prev来反转其方向。因此,将curr->next设置为prev。 - 将
prev设置为curr,将其向前移动一个位置。 - 将
curr设置为next,将其向前移动一个位置。
- 将
递归算法
-
将列表分为两部分:第一个节点,即
head节点,以及其余的链接列表。 -
调用
reverse(head->next),即,反向链接列表的其余部分,并将反向链接列表存储为rev。 -
将
head附加到反向链接列表rev的末尾。 -
指向
head,即反向链接列表的尾部指向NULL。
使用堆栈的反向链接列表
-
初始化指向链接列表的
head的指针curr。 -
遍历链表,并将每个节点一一插入。
-
将
head更新到链表中的最后一个节点,即堆栈中的第一个节点。 -
开始一个接一个地从堆栈中弹出节点,并将其附加到反向链表的末尾。
-
将最后一个节点的下一个指针更新为
NULL。
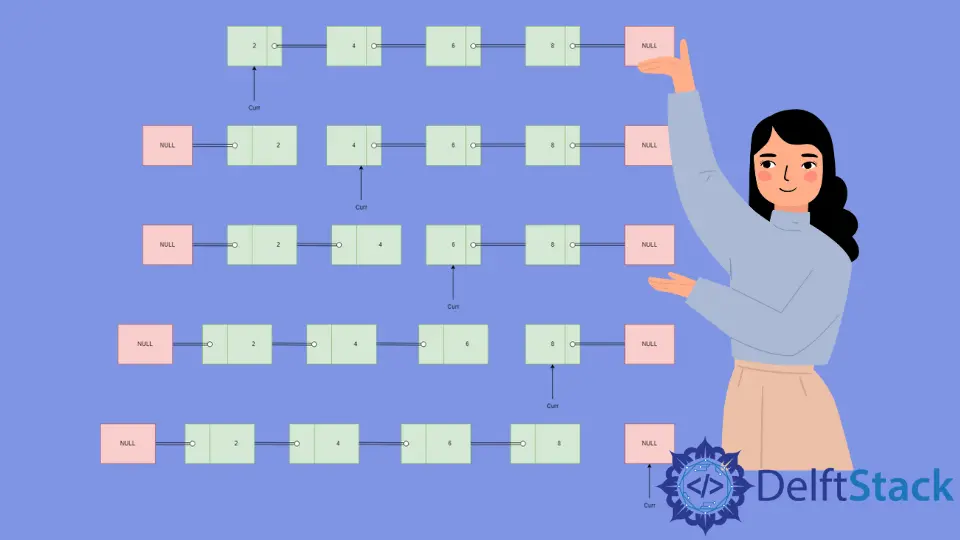
链表反转图解
-
初始化
curr以指向头部,即节点2和prev以及curr的数据为NULL。 -
将
next指向curr->next,其值等于4。 -
将
curr->next设置为prev,以获得以2为首的反向链接列表。 -
将
prev移至curr,即数据为2的节点,将curr移至next,即数据为4的节点。 -
将
next指向curr->next,其值等于6。 -
将
curr->next设置为prev,以获得以2和4为反向节点,以4为首的反向链表。 -
将
prev移至curr,即数据为4的节点,将curr移至next,即数据为6的节点。 -
将
next指向curr->next,其值等于8。 -
将
curr->next设置为prev,以获得以2,4和6为反向节点且以6为首的反向链表。 -
将
prev移至curr,即数据为6的节点,将curr移至next,即数据为8的节点。 -
将
next指向curr->next,即NULL。 -
将
curr->next设置为prev,以2,4,6和8作为反向节点,以8作为头获得反向链表。 -
将
prev移至curr,即数据为8的节点,将curr移至NULL,算法终止。
链表反转的实现
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* next;
Node(int x) {
this->data = x;
this->next = NULL;
}
};
void printList(Node* head) {
Node* curr = head;
while (curr != NULL) {
cout << curr->data << " ";
curr = curr->next;
}
}
Node* reverse(Node* head) {
Node* curr = head;
Node *prev = NULL, *next = NULL;
while (curr != NULL) {
next = curr->next;
curr->next = prev;
prev = curr;
curr = next;
}
head = prev;
return head;
}
Node* recursiveReverse(Node* head) {
if (head == NULL || head->next == NULL) return head;
Node* rest = recursiveReverse(head->next);
head->next->next = head;
head->next = NULL;
return rest;
}
void reverseLL(Node** head) {
stack<Node*> s;
Node* temp = *head;
while (temp->next != NULL) {
s.push(temp);
temp = temp->next;
}
*head = temp;
while (!s.empty()) {
temp->next = s.top();
s.pop();
temp = temp->next;
}
temp->next = NULL;
}
int main() {
Node* head = new Node(1);
head->next = new Node(2);
head->next->next = new Node(3);
head->next->next->next = new Node(4);
head->next->next->next->next = new Node(5);
head->next->next->next->next->next = new Node(6);
head = reverse(head);
printList(head);
cout << "\n";
head = recursiveReverse(head);
printList(head);
cout << "\n";
reverseLL(&head);
printList(head);
cout << "\n";
return 0;
}
链表反转算法复杂度
时间复杂度
- 平均情况
要反转完整的链表,我们必须访问每个节点,然后将其附加到反转表。因此,如果一个链表具有 n 个节点,则遍历的平均情况下时间复杂度约为 O(n)。时间复杂度约为 O(n)。
- 最佳情况
最佳情况下的时间复杂度是 O(n)。它与平均情况下的时间复杂度相同。
- 最坏情况
最差的时间复杂度是 O(n)。它与最佳情况下的时间复杂度相同。
空间复杂度
该遍历算法的空间复杂度为 O(1),因为除了临时指针外,不需要额外的空间。
作者: Harshit Jindal
Harshit Jindal has done his Bachelors in Computer Science Engineering(2021) from DTU. He has always been a problem solver and now turned that into his profession. Currently working at M365 Cloud Security team(Torus) on Cloud Security Services and Datacenter Buildout Automation.
LinkedIn

