树形选择排序
树形选择排序是一种在线排序算法,它使用二叉搜索树数据结构来存储元素。它使用二叉搜索树数据结构来存储元素。通过对二叉搜索树进行顺序内遍历,可以按排序顺序检索元素。由于是在线排序算法,所以插入的元素始终保持排序的顺序。
树形选择排序算法
假设我们有一个包含 n 个元素的未排序数组 A[]。
TreeSort()
-
将数组中的元素插入到二叉搜索树中,构建二叉搜索树。
-
在树上进行顺序遍历,将元素按排序顺序取回。
Insert()
-
创建一个 BST 节点,其值等于数组元素
A[i]。 -
Insert(node,key)。-
如果
root为null, 返回新形成的节点。 -
如果
root➡data<key,root➡right=insert(root➡right,key) -
如果
root➡data>key,root➡left=insert(root➡left,key)
-
-
返回指向原始根的指针。
Inorder()
-
遍历左侧子树。
-
访问根部。
-
遍历右边的子树。
树形选择排序示例
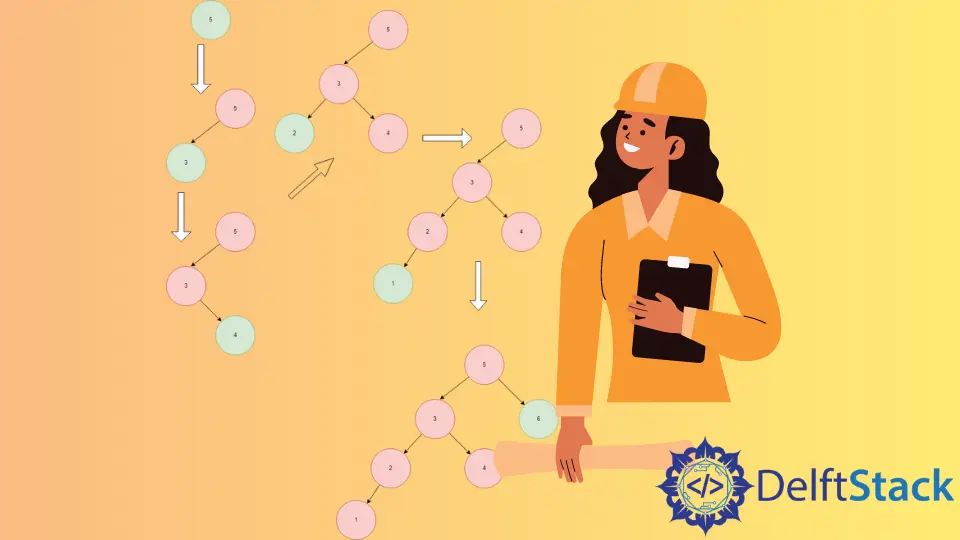
假设我们有一个数组:(5, 3, 4, 2, 1, 6). 我们将使用插入排序算法对其进行排序。
首先,我们通过创建根节点 5 来初始化 BST。
3 比 5 小,所以它被插入 5 的左边;4 比 5 小,但比 3 大,所以它被插入 3 的右边。
4 比 5 小,但比 3 大,所以它被插入到 3 的右边,但 4 的左边。
2 是当前树中最小的元素,所以它被插入到最左边的位置。
1 是当前树中最小的元素,所以它被插入到最左边的位置。
6 是当前树中最大的元素,所以它被插入到最右边的位置。
建立完二叉搜索树后,我们对树进行顺序遍历,得到最终的排序数组 (1, 2, 3 ,4, 5, 6)。
树形选择排序算法的实现
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int key;
Node *left, *right;
};
Node *newNode(int item) {
Node *temp = new Node;
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void inorder(Node *root, int arr[], int &i) {
if (root != NULL) {
inorder(root->left, arr, i);
arr[i++] = root->key;
inorder(root->right, arr, i);
}
}
Node *insertintoBST(Node *node, int key) {
if (node == NULL) return newNode(key);
if (key < node->key)
node->left = insertintoBST(node->left, key);
else if (key > node->key)
node->right = insertintoBST(node->right, key);
return node;
}
void treeSort(int arr[], int n) {
Node *root = NULL;
root = insertintoBST(root, arr[0]);
for (int i = 1; i < n; i++) root = insertintoBST(root, arr[i]);
int i = 0;
inorder(root, arr, i);
}
int main() {
int n = 6;
int arr[6] = {5, 3, 4, 2, 1, 6};
cout << "Input array: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << "\n";
treeSort(arr, n); // Sort elements in ascending order
cout << "Output array: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << "\n";
}
树形选择排序算法的复杂度
时间复杂度
- 平均情况
在平均情况下,在 BST 中插入 n 节点的时间复杂度为 O(nlogn)。当形成的 BST 是一个平衡的 BST 时,就会出现这种情况。因此,时间复杂度为 [Big Theta]:O(nlogn)。
- 最坏情况
最坏的情况发生在对数组进行排序,并形成一棵最大高度为 O(n) 的不平衡二叉搜索树。遍历需要 O(n) 时间,插入需要 O(n2)时间,而高度 logn 的常规 BST 的遍历时间为 O(logn)。最坏情况下的时间复杂度为 [Big O]:O(n2)。
使用 AVL 树、红黑树等自平衡数据结构,可以将其降低到 O(nlogn)。
- 最佳情况
当形成的二叉搜索树是平衡的时候,就会出现最好的情况。最佳情况下的时间复杂度为 [Big Omega]:O(nlogn)。它与平均情况下的时间复杂度相同。
空间复杂度
该算法的空间复杂度为 O(n),因为要为二叉搜索树内的每个元素创建 n 个节点。
Harshit Jindal has done his Bachelors in Computer Science Engineering(2021) from DTU. He has always been a problem solver and now turned that into his profession. Currently working at M365 Cloud Security team(Torus) on Cloud Security Services and Datacenter Buildout Automation.
LinkedIn
