快速排序
快速排序是一种基于分而治之算法的高效排序算法。快速排序的工作原理是围绕一个选定的中轴元素将数组分割成两个部分。它将较小的元素移到中轴的左侧,较大的元素移到右侧。之后,左右两部分递归排序,对整个数组进行排序。之所以称为快速排序,是因为它比常见的排序算法快了约 2 或 3 倍。快速排序广泛应用于数据结构内部的信息搜索和数值计算。
快速排序算法
假设我们有一个无序数组 A[],包含 n 个元素。取两个变量 beg 和 end,然后存储开始和结束元素的索引。
Partition()
-
选择最后一个元素(可以是任何元素,取决于实现)作为中轴元素。
-
初始化指针
i的值为beg - 1,这样我们就可以把小于中轴的元素移到数组的起始位置。 -
迭代遍历数组,并对每个元素做如下操作。
-
如果元素
A[i]<pivot,则递增i并将A[i]与A[j]交换。 -
将
A[i]与A[end]互换,使中轴元素处于正确的位置。 -
返回中轴元素的索引。
QuickSort()
-
选择中轴索引
pi。 -
围绕中轴索引对数组进行分区。
-
在中轴元素的左侧
arr[beg,...,pi]递归排序元素。 -
在中轴元素的右侧
arr[pi+1,...,end]上对元素进行递归排序。
快速排序示例
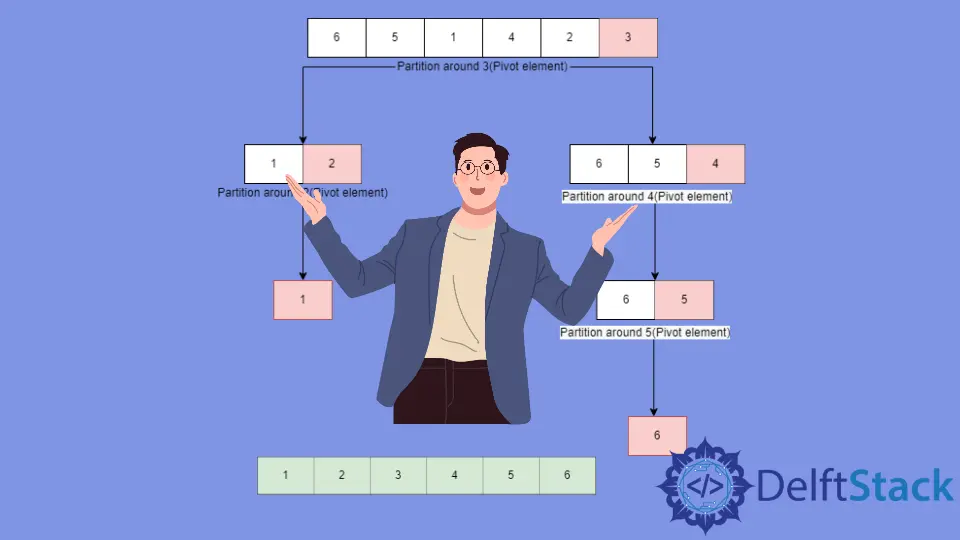
假设我们有一个数组:(6,5,1,4,2,3)。我们将使用快速排序算法对其进行排序。
-
首先选择
3作为中轴元素,将数组分成两个子部分(1,2)- 较小的元素,和(6,5,4)- 较大的元素。然后将3放在其排序位置。然后对形成的两个子数组进行递归排序。 -
对于子数组
(1,2),选择2作为中轴元素并放在正确的位置,然后形成已经排序的子数组(1)。 -
对于子数组
(6,5,4),4被放在排序后的位置,形成子数组(6,5),然后递归排序。 -
对于子数组
(6,5),选择5作为支点,放到正确的位置,从而得到(6)作为新的子数组。单元素子数组(6)已经被排序了。 -
最后,我们得到排序后的数组为
(1,2,3,4,5,6)。
快速排序算法实现
#include <bits/stdc++.h>
using namespace std;
int partition(int arr[], int beg, int end) {
// Select the last element as pivot element
int pivot = arr[end];
int i = (beg - 1);
// Move smaller elements to left side and larger on right side
for (int j = beg; j < end; j++) {
if (arr[j] <= pivot) {
i++;
swap(arr[i], arr[j]);
}
}
swap(arr[i + 1],
arr[end]); // Move pivot element to its right position in array
return (i + 1);
}
void quickSort(int arr[], int beg, int end) {
if (beg < end) {
int pi = partition(arr, beg, end);
quickSort(arr, beg,
pi - 1); // Recursive Sort element on left side of partition
quickSort(arr, pi + 1,
end); // Recursive Sort element on right side of partition
}
}
int main() {
int n = 6;
int arr[6] = {5, 3, 4, 2, 1, 6};
cout << "Input array: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << "\n";
quickSort(arr, 0, n - 1); // Sort elements in ascending order
cout << "Output array: ";
for (int i = 0; i < n; i++) {
cout << arr[i] << " ";
}
cout << "\n";
}
快速排序算法的复杂度
时间复杂度
- 平均情况
快速排序所需时间由以下递推关系给出。
T(n) = T(k) + T(n-k-1) + θ(n)
这里的 k 代表比中轴元素小/大的元素数,这个递归关系的结果是 T(n) = nLogn。
这个递归关系的结果给出了 T(n)=nLogn.当我们得到随机的不均衡分区时,就会出现平均情况。时间复杂度是 [Big Theta]:O(nLogn)。
- 最坏情况
T(n) = T(n-1) + θ(n)
最坏的情况是,中轴元素总是数组中最大或最小的元素。在这种情况下,所有元素都落在一个子数组中,必须进行最大的 n 调用。最坏情况下的时间复杂度是[大 O]。O(n2)。
- 最佳情况
T(n) = 2T(n/2) + θ(n)
最好的情况是,当所选的中轴元素总是中间元素,或者当两个分区均匀平衡时,即大小相差 1 或更小。最佳情况下的时间复杂度为 [Big Omega]:O(nLogn)。
空间复杂度
快速排序算法的平均情况下空间复杂度为 O(Logn)。这是递归栈所需要的空间。但在最坏的情况下,当排序一个数组需要 n 递归时,空间复杂度是 O(n)。
Harshit Jindal has done his Bachelors in Computer Science Engineering(2021) from DTU. He has always been a problem solver and now turned that into his profession. Currently working at M365 Cloud Security team(Torus) on Cloud Security Services and Datacenter Buildout Automation.
LinkedIn

