在 Base R 中执行 K-Means 聚类
本文展示了如何在 R 中执行 K-means 聚类。包括可视化在内的所有步骤都使用基本 R 函数进行了演示。
关于 R 中的 K-Means 聚类
K-means 聚类是一种无监督统计技术，可将数据集划分为不相交的同质子组。
在进行 K-means 聚类时，我们必须牢记以下几点。
- 所有变量都必须是数字，因为方法取决于计算方法和距离。用数字编码的因子数据不是数字。
- 我们的数据集中应该没有因变量。
- 该方法将每个观测值分配给一个集群。因此，它对异常值和数据变化很敏感。
- 它适用于不相交的集群，但在数据具有重叠集群的情况下效果不佳。
R 中的 kmeans() 函数
Base R 包含用于 K-means 聚类的 kmeans() 函数。
我们将使用以下参数。
- 第一个参数是数据。
- 第二个参数，
centers，是集群的数量。 - 第三个参数，
nstart，是用不同的初始质心重复聚类的次数。
K-means 算法给出了组内总平方和的局部最优值。这个局部最优取决于随机选择的初始质心。
因此，nstart 用于重复聚类。该函数返回总数最低的集群。
R 中的 K-Means 模型
为了创建 K-means 模型，我们将创建一个包含两个变量和三个集群的数据框。
示例代码：
# Vectors for the data frame.
set.seed(4987)
M1 = rnorm(13)
set.seed(9874)
M2 = rnorm(11) + 3
set.seed(8749)
N1 = runif(13)
set.seed(7498)
N2 = runif(11) -2
set.seed(6237)
M3 = rnorm(14) - 6
set.seed(2376)
N3 = runif(14) + 1
# Data frames.
df1 = data.frame(M1, N1)
colnames(df1) = c("M","N")
df2 = data.frame(M2, N2)
colnames(df2) = c("M","N")
df3 = data.frame(M3,N3)
colnames(df3) = c("M","N")
DF = rbind(df1, df2, df3) # Final data frame.
让我们可视化这些数据。
示例代码：
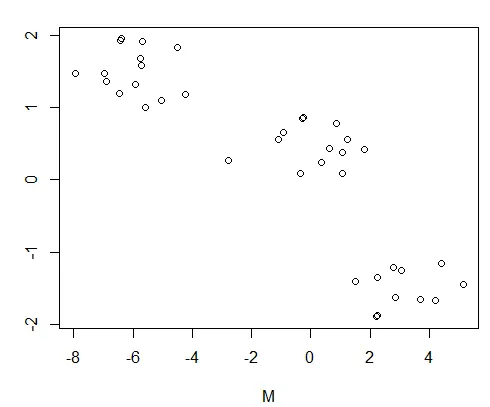
plot(DF)
数据框图：
我们现在将创建 K-means 模型。
示例代码：
# The K-means model.
set.seed(9944)
km_1 = kmeans(DF, centers=3, nstart = 20)
我们模型中的变量 cluster 保存了算法得出的集群标签。变量 tot.withinss 保存组内总平方和。
让我们看看算法分配的集群标签。唯一重要的是属于一个集群的观察应该具有相同的标签。
示例代码：
km_1$cluster
输出：
> km_1$cluster
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2
我们发现集群被正确识别。
簇数 (K)
实际上，我们可能不知道我们的数据有多少簇。在这种情况下，我们需要尝试不同的 K 值，看看哪个值给出了相当低的组内总平方和。
问题是，随着 K 的增加，我们将在数据点附近创建更多的质心，并且组内总平方和将下降。
因此，我们需要找到一个相当小的 K 来发现数据中存在的集群，但不会过度拟合。
通常的方法称为肘弯法。我们从 1 开始为不同的 K 值创建模型，并绘制每个模型的组内总平方和。
我们在图中寻找直线斜率变化最大的点。它看起来像手臂的肘关节。为模型选择了那个特定的 K。
在示例代码中，我们将使用一个循环来创建模型，并使用一个向量来存储每个模型的组内总平方和。
示例代码：
# Create a vector to hold the total within-group sum of squares of each model.
vec_ss = NULL
# Create a loop that creates K-means models with increasing value of K.
# Add the total within group sum of squares of each model to the vector.
for(k in 1:20){
set.seed(8520)
vec_ss[k] = kmeans(DF, centers=k, nstart=18)$tot.withinss
}
# View the vector with the total sum of squares of the 20 models.
vec_ss
# Plot the values of the vector.
plot(vec_ss, type="l", xaxp=c(0,20,10), xlab="K", ylab="Total within-group-ss")
输出：
用于估计正确 K 的肘弯图：
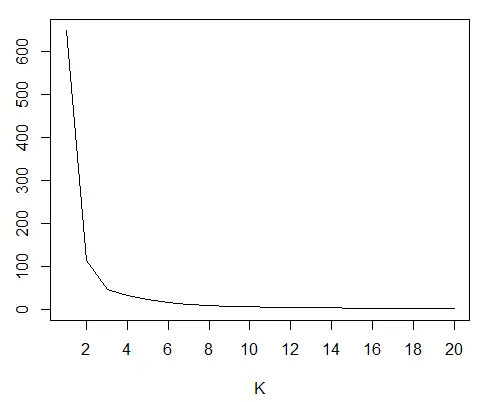
肘部弯曲在 K = 3，这是我们数据的正确值。
在 R 中可视化集群
我们可以用散点图可视化集群。颜色参数 col 区分集群。
簇编号为 1、2、3； col 参数从现有调色板中为相应的点选择这些颜色。
示例代码：
plot(DF, col=km_1$cluster, pch=19)
输出：
K 均值聚类图。
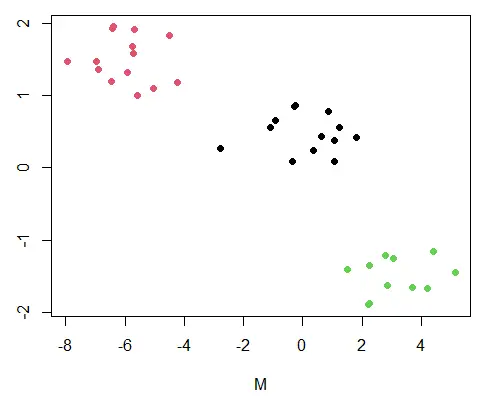
当有两个以上的变量时，我们可以执行以下操作。
- 创建 K-means 模型并获得
cluster向量。 - 创建一个主成分模型。
- 绘制前两个主成分。
示例代码：
# First, we will add a third variable to our data frame.
O1 = rnorm(13,10,2)
O2 = rnorm(11, 5,3)
O3 = rnorm(14,0,2)
O = as.data.frame(c(O1,O2,O3))
colnames(O) = "O"
DF = cbind(DF, O)
##################################
# The K-means model.
km_2 = kmeans(DF, centers=3, nstart=20)
# The PCA model.
pca_mod = prcomp(DF)
# Visualize the first two principal components with the cluster labels as color.
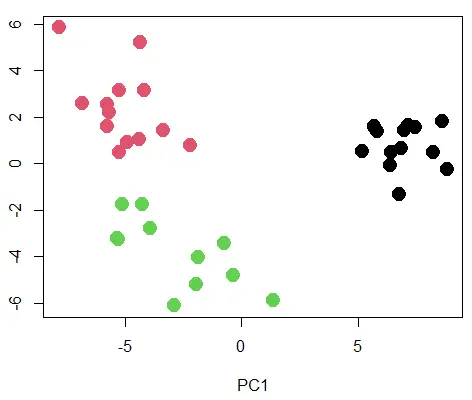
plot(pca_mod$x[,1:2], col=km_2$cluster, pch=19, cex=2)
输出：
带有聚类的 PCA 散点图。
其他实际考虑
kmeans()函数使用随机数生成初始质心。使用set.seed()函数使我们的代码可重现。- 我们必须删除具有缺失值的观测值才能使用
kmeans()函数。为此，我们可以使用na.omit()函数。 - 我们可以选择使用
scale()函数缩放每个变量，使其具有0的mean和1的sd。
参考
统计学习简介一书介绍了使用 R 的 K-means 聚类。
Jesse is passionate about data analysis and visualization. He uses the R statistical programming language for all aspects of his work.