Python 中的平滑数据

1. 在 Python 中使用 scipy.signal.savgol_filter() 方法平滑数据
2. 在 Python 中使用 numpy.convolve 方法平滑数据
3. 在 Python 中使用 statsmodels.kernel_regression 平滑数据

Python 在数据分析和可视化方面有着广泛的应用。当我们分析包含许多观测值的海量数据集时，我们可能会遇到必须平滑图形上的曲线以更仔细地研究最终图的情况。我们将讨论如何使用不同的方法在 Python 中实现这一点。

在 Python 中使用 scipy.signal.savgol_filter() 方法平滑数据

Savitzky-Golay 滤波器是一种数字滤波器，它使用数据点来平滑图形。它使用最小二乘法创建一个小窗口并对该窗口的数据应用多项式，然后使用该多项式来假设特定窗口的中心点。接下来，将窗口移动一个数据点，并迭代该过程，直到所有邻居彼此相对调整。

我们可以使用 scipy.signal.savgol_filter() 函数在 Python 中实现这一点。

请参考以下示例。

import numpy as np
from scipy.signal import savgol_filter
import matplotlib.pyplot as plt

x = np.linspace(0,2*np.pi,100)
y = np.sin(x) + np.random.random(100) * 0.2
yhat = savgol_filter(y, 51, 3)

plt.plot(x, y)
plt.plot(x,yhat, color='green')
plt.show()

输出：

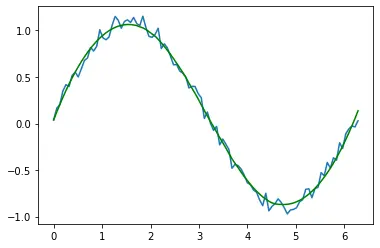
在上面的例子中，我们使用过滤方法来平滑要绘制在 y 轴上的数据。我们绘制了原始数据和平滑数据，以便你观察差异。

在 Python 中使用 numpy.convolve 方法平滑数据

numpy.convolve() 给出两个一维序列的离散线性卷积。我们将使用它来创建可以过滤和平滑数据的移动平均线。

这不被认为是一个好方法。

例如，

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0,2*np.pi,100)
y = np.sin(x) + np.random.random(100) * 0.8

def smooth(y, box_pts):
    box = np.ones(box_pts)/box_pts
    y_smooth = np.convolve(y, box, mode='same')
    return y_smooth

plt.plot(x, y)
plt.plot(x, smooth(y,3))
plt.plot(x, smooth(y,19))

输出：

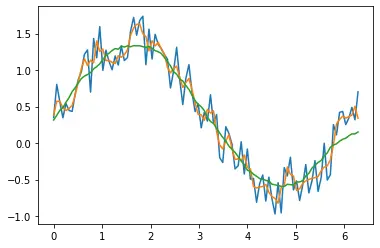
在上面的例子中，我们绘制了两个时间增量为 3 和 19 的移动平均线。我们在图中绘制了它们。

我们也可以使用其他方法来计算移动平均线。

在 Python 中使用 statsmodels.kernel_regression 平滑数据

核回归计算条件均值 E[y|X]，其中 y = g(X) + e 并拟合模型。它可用于根据控制变量平滑数据。

为此，我们必须使用 statsmodels 模块中的 KernelReg() 函数。

例如，

from statsmodels.nonparametric.kernel_regression import KernelReg
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0,2*np.pi,100)
y = np.sin(x) + np.random.random(100) * 0.2

kr = KernelReg(y,x,'c')
plt.plot(x, y, '+')
y_pred, y_std = kr.fit(x)

plt.plot(x, y_pred)
plt.show()

输出：

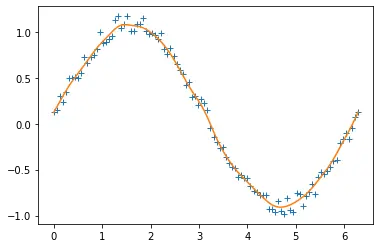
请注意，此方法产生了良好的结果，但被认为非常慢。我们也可以使用傅立叶变换，但它只适用于周期性数据。