在 Python 中使用 RMSE

1. Python 中均方根误差的公式
2. 在 Python 中使用 NumPy 计算 RMSE
3. 在 Python 中使用 scikit-learn 库计算 RMSE

RMS（均方根 root mean square），也称为二次平均，是一系列数字平方的算术平均值的平方根。

RMSE（均方根误差）为我们提供了实际结果与模型计算结果之间的差异。它定义了我们的模型（使用定量数据）的质量，我们的模型预测的准确度，或者我们模型中的错误百分比。

RMSE 是评估监督机器学习模型的方法之一。RMSE 越大，我们的模型就越不准确，反之亦然。

使用 NumPy 库或 scikit-learn 库有多种方法可以在 Python 中找到 RMSE。

Python 中均方根误差的公式

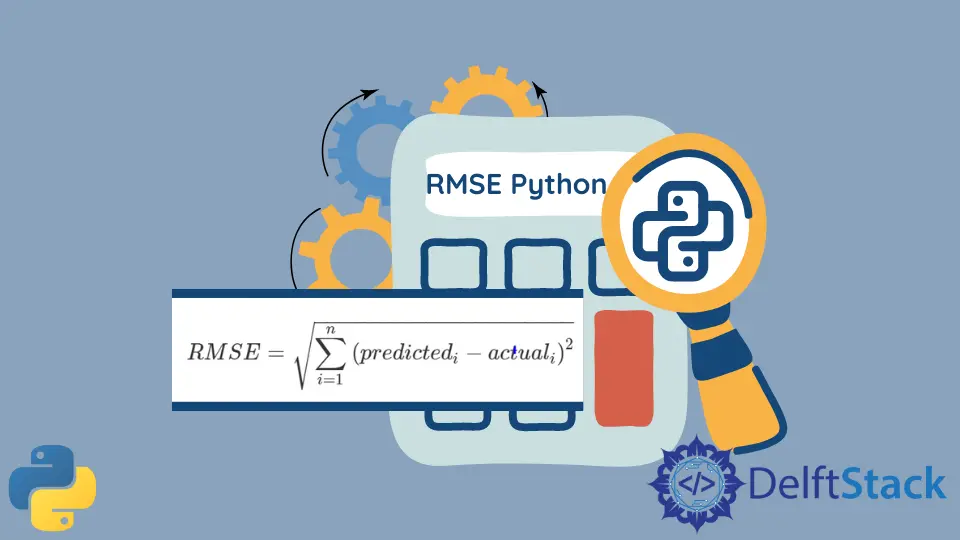
计算 RMSE 背后的逻辑是通过以下公式：

$$
RMSE=\sqrt{\sum_{i=1}^n {(predicted_{i}-actual_{i})}^2}
$$

在 Python 中使用 NumPy 计算 RMSE

NumPy 是处理大数据、数字、数组和数学函数的有用库。

使用这个库，当给定 actual 和 predicted 值作为输入时，我们可以轻松计算 RMSE。我们将使用 NumPy 库的内置函数来执行不同的数学运算，如平方、均值、差值和平方根。

在下面的例子中，我们将通过首先计算 actual 和 predicted 值之间的 difference 来计算 RMSE。我们计算该差异的平方，然后取平均值。

直到这一步，我们将获得 MSE。为了得到 RMSE，我们将取 MSE 的平方根。

示例代码：

#python 3.x
import numpy as np
actual = [1,2,5,2,7, 5]
predicted = [1,4,2,9,8,6] 
diff=np.subtract(actual,predicted)
square=np.square(diff)
MSE=square.mean()
RMSE=np.sqrt(MSE)
print("Root Mean Square Error:", RMSE)

输出：

#python 3.x
Root Mean Square Error: 3.265986323710904

在 Python 中使用 scikit-learn 库计算 RMSE

在 Python 中计算 RMSE 的另一种方法是使用 scikit-learn 库。

scikit-learn 对机器学习很有用。该库包含一个名为 sklearn.metrics 的模块，其中包含内置的 mean_square_error 函数。

我们将从这个模块导入函数到我们的代码中，并从函数调用中传递 actual 和 predicted 值。该函数将返回 MSE。为了计算 RMSE，我们将取 MSE 的平方根。

示例代码：

#python 3.x
from sklearn.metrics import mean_squared_error
import math
actual = [1,2,5,2,7, 5]
predicted = [1,4,2,9,8,6]
MSE = mean_squared_error(actual, predicted)
RMSE = math.sqrt(MSE)
print("Root Mean Square Error:",RMSE)

输出：

#python 3.x
Root Mean Square Error: 3.265986323710904