Python 中的 Lasso 回归

1. Python 中的 Lasso 回归
2. 在 Python 中实现 Lasso 回归

回归是一种统计技术，可确定因变量和自变量之间的关系。我们可以使用回归作为机器学习模型在 Python 中进行预测分析。

线性回归和逻辑回归是最常见的回归技术。它已经发展，现在已经引入了改进的回归版本。

该技术的准确性可能存在一些问题。

已经讨论并证明了传统的回归技术在自变量数量增加时会导致过度拟合的问题，同时增加多项式的次数。

过度拟合的另一个重要因素是嘈杂和不一致的数据，导致结果不准确。

引入正则化来解决这个问题。Lasso 回归就是这样一种技术，它在预测分析中使用正则化和变量选择。

Python 中的 Lasso 回归

Lasso 回归有助于处理数据集中具有更多不相关特征的情况。我们需要将这些特征的系数降低到最低限度，以消除它们对预测的影响。

Lasso 回归在成本函数中引入了一个称为 L1 惩罚的值。在梯度优化过程中，不相关特征的权重通过 L1 惩罚降低到最小值（几乎为 0）。

函数中不考虑这些缩小的权重以消除它们的相关性。

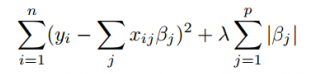
Lasso 回归的数学方程如上图所示。这里，λ的值是决定收缩量的收缩参数。

更高的值意味着更多的偏差和更少的方差。对于λ = 0，所有特征都被认为是等价的，无穷大的值决定不考虑任何特征。

用参数诱导 L1 惩罚的主要概念是在参数值增加时降低特征的权重。

在 Python 中实现 Lasso 回归

我们使用 sklearn.linear_model.Lasso 类在 Python 中实现 Lasso 回归。我们可以使用这个类创建一个模型，并将它与所需的训练和测试数据一起使用来进行预测。

它采用参数 alpha，即乘以 L1 惩罚的常数值。该对象还接受其他参数，如 fit_intercept、normalize、precompute、copy_X 等。

让我们用 Python 实现一个 Lasso 回归的例子。

from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn import datasets

data = datasets.load_boston()
x_data = data.data
y_data = data.target

train_x, test_x, train_y, test_y = train_test_split(x_data, y_data, test_size=0.3, random_state=42)

lasso = Lasso(alpha=1.0)
lasso.fit(train_x, train_y)
print(lasso.score(test_x, test_y)*100)

输出：

65.59060829154339

在上面的示例中，我们从 sklearn 模块加载了一个样本数据集，并将其拆分为 x_data 和 y_data。我们使用 train_test_split 类将数据集分为训练数据集和测试数据集。

我们使用训练数据集使用 fit() 函数训练 Lasso 回归模型。然后，我们使用 score() 函数检查预测数据的分数。

输出显示该模型以 65.59% 的准确率预测数据。

我们可以执行交叉验证来找到 Lasso 模型的 alpha 参数的最佳值。

我们可以导入 sklearn.linear_model.LassoCV 类。然后，我们可以指定交叉验证技术中的折叠数。

请参阅下面的代码。

from sklearn.linear_model import Lasso
from sklearn.model_selection import train_test_split
from sklearn import datasets

data = datasets.load_boston()
x_data = data.data
y_data = data.target

train_x, test_x, train_y, test_y = train_test_split(x_data, y_data, test_size=0.3, random_state=42)

from sklearn.linear_model import LassoCV
lassocv = LassoCV(cv=5, random_state=0, max_iter=10000)
lassocv.fit(train_x, train_y)
al = lassocv.alpha_
print(al)

lasso = Lasso(alpha=al)
lasso.fit(train_x, train_y)
print(lasso.score(test_x, test_y)*100)

输出：

0.7051444556162024
67.48582731460068

在上面的例子中，我们找到了 alpha 值的最佳值，然后用这个值来训练和测试之前的模型。新 alpha 值的模型准确率为 67.48%。