使用 Python 实现高通滤波器
Vaibhav Vaibhav
2024年2月15日
高通滤波器是限制低于预定义阈值频率或截止频率的信号移动的滤波器。频率大于或等于阈值的信号畅通无阻地通过滤波器。此动作会衰减低频信号。高通滤波器过滤掉不需要的噪音,例如声音。
在本文中,我们将学习如何使用 Python 实现高通滤波器。
使用 Python 实现高通滤波器
高通滤波器的实现使用了 4 个 Python 模块,即 numpy、pandas、scipy 和 matplotlib。
numpy 模块是一个强大的 Python 模块,具有丰富的实用程序,可用于处理大型多维矩阵和数组。这些实用程序有助于无缝地对矩阵执行复杂和直接的数学运算。这些实用程序针对输入进行了优化和高度动态化。
要安装最新版本的 numpy 模块,请使用以下 pip 命令之一。
pip install numpy
pip3 install numpy
pandas 模块是一个功能强大且灵活的开源数据分析和数据操作模块,用 Python 编写。
要安装 pandas 模块,请使用以下 pip 命令之一。
pip install pandas
pip3 install pandas
scipy 模块是用于科学和技术计算的开源 Python 模块。
要安装 scipy 模块,请使用以下 pip 命令之一。
pip install scipy
pip3 install scipy
而且,matplotlib 模块是一个全面且优化的 Python 库,用于数据的图形可视化。
要安装最新版本的 matplotlib 模块,请使用以下 pip 命令之一。
pip install matplotlib
pip3 install matplotlib
现在我们已经完成了关于库的简要介绍,让我们看看高通滤波器的 Python 代码。
import numpy as np
import pandas as pd
from scipy import signal
import matplotlib.pyplot as plt
def sine_generator(fs, sinefreq, duration):
T = duration
n = fs * T
w = 2.0 * np.pi * sinefreq
t_sine = np.linspace(0, T, n, endpoint=False)
y_sine = np.sin(w * t_sine)
result = pd.DataFrame({"data": y_sine}, index=t_sine)
return result
def butter_highpass(cutoff, fs, order=5):
nyq = 0.5 * fs
normal_cutoff = cutoff / nyq
b, a = signal.butter(order, normal_cutoff, btype="high", analog=False)
return b, a
def butter_highpass_filter(data, cutoff, fs, order=5):
b, a = butter_highpass(cutoff, fs, order=order)
y = signal.filtfilt(b, a, data)
return y
fps = 30
sine_fq = 10
duration = 10
sine_5Hz = sine_generator(fps, sine_fq, duration)
sine_fq = 1
duration = 10
sine_1Hz = sine_generator(fps, sine_fq, duration)
sine = sine_5Hz + sine_1Hz
filtered_sine = butter_highpass_filter(sine.data, 10, fps)
plt.figure(figsize=(20, 10))
plt.subplot(211)
plt.plot(range(len(sine)), sine)
plt.title("Generated Signal")
plt.subplot(212)
plt.plot(range(len(filtered_sine)), filtered_sine)
plt.title("Filtered Signal")
plt.show()
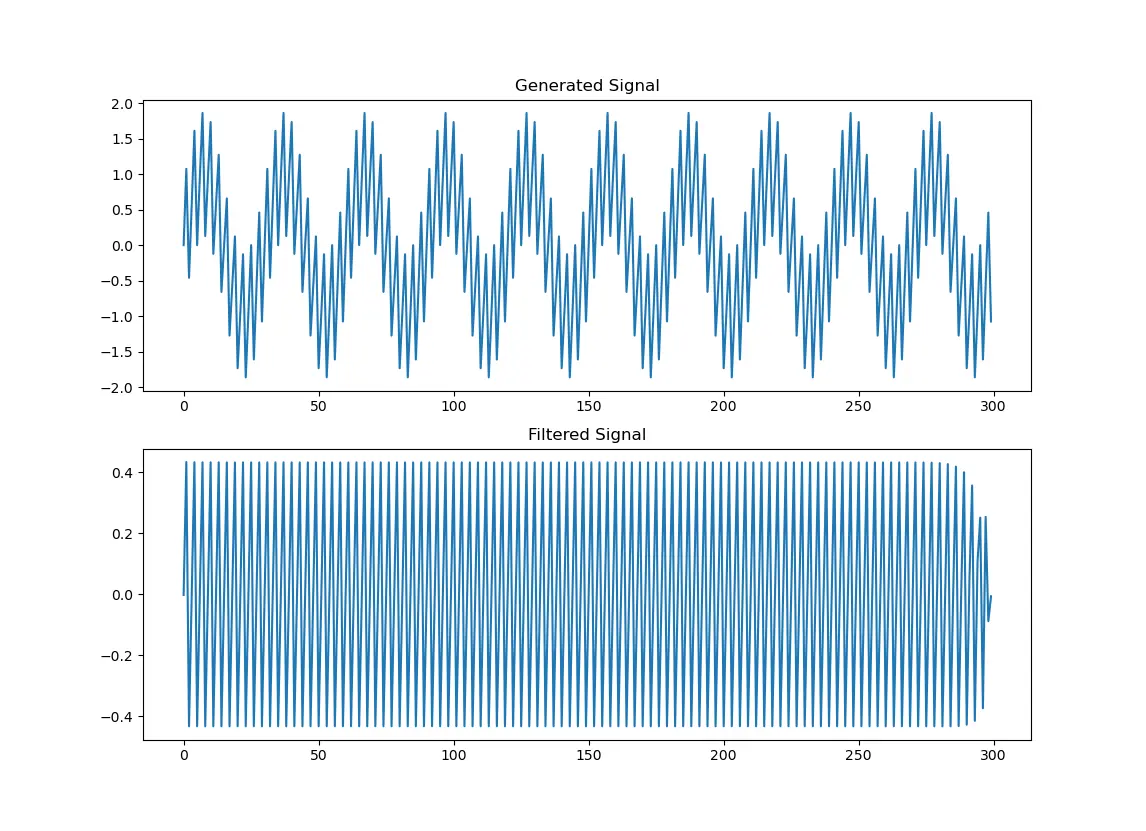
在上面的代码中,正弦频率或 sine_fq 值应以赫兹或 Hz 为单位,持续时间或 duration 应以秒或 sec 为单位。生成的信号是原始信号,滤波后的信号是高通滤波器形成的信号。生成的图表显示了两者之间的差异。
作者: Vaibhav Vaibhav
