Python 中的曲线曲率
Manav Narula
2021年8月10日
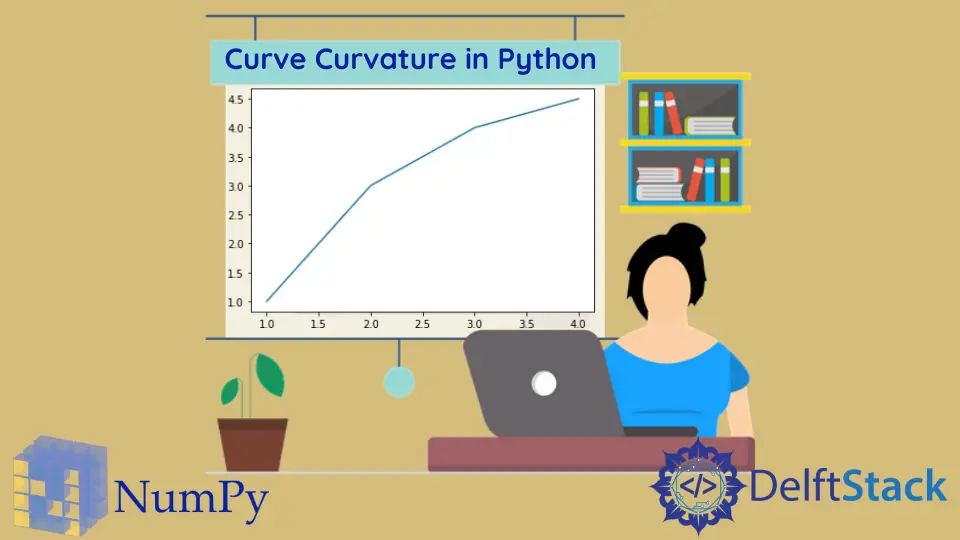
曲率是曲线偏离直线的量度。例如,圆的曲率是半径的倒数,而直线的曲率是 0。
在本教程中,我们将学习如何使用 numpy 模块在 Python 中计算曲线的曲率。我们还将计算其他量,例如速度,加速度等。你可以在下面的图片中找到必要的公式。
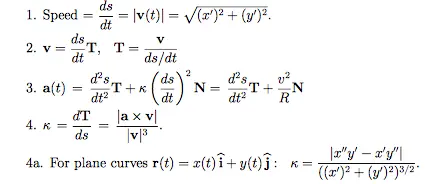
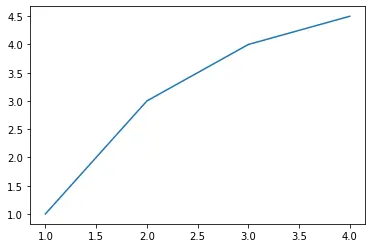
我们将使用以下曲线。
import numpy as np
import matplotlib.pyplot as plt
coordinates = np.array(
[[1, 1], [1.5, 2], [2, 3], [2.5, 3.5], [3, 4], [3.5, 4.25], [4, 4.5]]
)
plt.plot(coordinates[:, 0], coordinates[:, 1])
输出:
对于与曲线有关的此类问题,我们需要计算给定曲线在每个点的导数。在这种情况下使用 numpy.gradient() 方法,该方法返回 N 维数组的梯度。
在下面的代码中,我们计算所有点的曲线速度。
x_t = np.gradient(coordinates[:, 0])
y_t = np.gradient(coordinates[:, 1])
vel = np.array([[x_t[i], y_t[i]] for i in range(x_t.size)])
print(vel)
输出:
[[0.5 1. ]
[0.5 1. ]
[0.5 0.75 ]
[0.5 0.5 ]
[0.5 0.375]
[0.5 0.25 ]
[0.5 0.25 ]]
在计算速度之后,我们继续进行速度。现在,速度就是速度的模数。但是,应该知道,到目前为止,所有事物都是 t 的函数(t 表示时间间隔)。因此,我们将在每一秒的时间间隔内将速度表示为数值的 numpy 数组。
请参见下面的代码。
speed = np.sqrt(x_t * x_t + y_t * y_t)
print(speed)
输出:
[1.11803399 1.11803399 0.90138782 0.70710678 0.625 0.55901699
0.55901699]
现在,为了计算切线,我们将执行一些变换,以确保速度和速度的大小相同。同样,我们需要能够将矢量值速度函数除以标量速度数组。
tangent = np.array([1 / speed] * 2).transpose() * vel
print(tangent)
输出:
[[0.4472136 0.89442719]
[0.4472136 0.89442719]
[0.5547002 0.83205029]
[0.70710678 0.70710678]
[0.8 0.6 ]
[0.89442719 0.4472136 ]
[0.89442719 0.4472136 ]]
同样,我们现在可以隔离切线的分量并计算其梯度以找到法线向量。
现在,我们将在下面的代码中实现提供的曲率公式。
ss_t = np.gradient(speed)
xx_t = np.gradient(x_t)
yy_t = np.gradient(y_t)
curvature_val = np.abs(xx_t * y_t - x_t * yy_t) / (x_t * x_t + y_t * y_t) ** 1.5
print(curvature_val)
输出:
[0. 0.04472136 0.17067698 0.26516504 0.256 0.17888544
0. ]
作者: Manav Narula
Manav is a IT Professional who has a lot of experience as a core developer in many live projects. He is an avid learner who enjoys learning new things and sharing his findings whenever possible.
LinkedIn