MATLAB fzero 函数
本教程将讨论使用 MATLAB 中的 fzero() 函数查找非线性函数的根。
MATLAB fzero() 函数
fzero() 函数用于查找非线性函数的根。该函数使用不同的插值方法,如割线法和二等分法来找到给定非线性函数的根。
fzero() 函数的基本语法如下。
roots = fzero(fun, x0);
上面的语法将返回从点 x0 开始的 fun 的根。例如,让我们通过在 3 附近找到 sine 函数的根来找到 pi 的值。
请参阅下面的代码。
clc
clear
f = @sin;
x0 = 3;
value = fzero(f,x0)
输出:
value = 3.1416
clc 和 clear 命令用于清除上述代码中的命令和工作区窗口。正如我们在输出中看到的,fzero() 函数返回的值大约等于 pi 的值。
除了传递单个点作为起点,我们还可以传递一个区间来找到给定非线性函数的根。例如,让我们在 1 到 3 的区间内找到 cosine 函数的根。
请参阅下面的代码。
clc
clear
f = @cos;
x0 = [1 3];
value = fzero(f,x0)
输出:
value = 1.5708
请注意,函数在区间端点处的值应在符号上有所不同;否则,将出现错误,如果出现错误,我们必须更改区间值之一的符号。在上面的代码中,我们没有使用具有不同符号的区间值,因为 cos(1) 和 cos(3) 符号已经不同。
请注意,我们要查找其根的输入函数应该只有一个参数,如果它有多个参数,我们必须在找到根之前传递其他参数的值。例如,让我们创建一个有两个参数的函数,传递一个参数的值,然后找到函数的根。
请参阅下面的代码。
clc
clear
f = @(x,c) cos(c*x);
c = 3;
f_1 = @(x) f(x,c);
x = fzero(f_1,0.1)
输出:
x = 0.5236
在上面的输出中,我们在 fzero() 函数中传递了 f_1 函数,因为 f 函数包含两个参数,除非我们传递一个参数的值,否则它的根不会被计算。
我们还可以使用 PlotFcns 参数在 fzero() 函数内设置一些其他选项作为当前点或函数值的图,使用 PlotFcns 设置默认设置为 2.2e-16 的容差值 TolX 参数,将在 fzero() 函数的每次迭代中使用 OutputFcn 参数调用的输出函数,使用 FunValCheck 参数检查目标函数的值,使用 Display 参数。
要设置选项,我们必须使用 optimset() 函数创建所有选项的结构。例如,让我们为非线性函数设置上述选项。
请参阅下面的代码。
clc
clear
f = @(x,c) cos(c*x);
c = 3;
f_1 = @(x) f(x,c);
options = optimset('PlotFcns',{@optimplotx,@optimplotfval},'Display','final','FunValCheck','on','TolX',1.1e-16);
x = fzero(f_1,0.1,options)
输出:
Zero found in the interval [-0.412, 0.612]
x = 0.5236

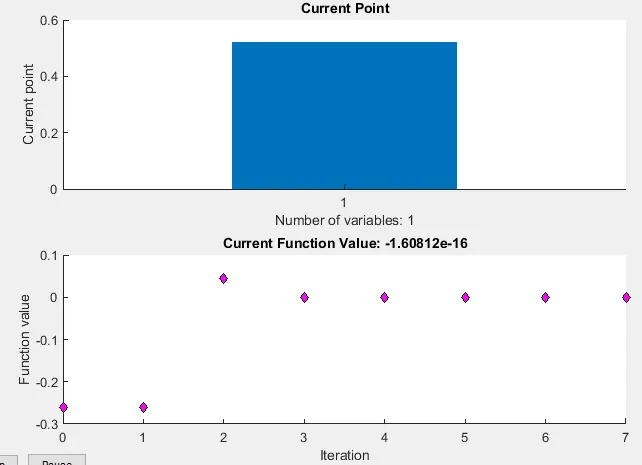
在上面的输出中,我们可以看到找到零的区间,我们还可以看到当前点的图和不同迭代的函数值图。
显示选项有四种类型 off 表示不输出,iter 表示每次迭代输出,final 表示仅最终输出,仅当函数不收敛时才通知输出。
我们可以将 FunValCheck 选项设置为 on 或 off,如果设置为 on,如果输出为无穷大、NaN 或复数,函数将显示错误,如果是设置为 off,将不会显示错误。
我们还可以通过使用 problem 参数将函数定义为问题结构来找到函数的根。
我们将使用 problem.objective 命令来定义函数。我们将使用 problem.x0 命令来初始化起点或间隔。
我们将使用 problem.solver 命令来定义求解方法。我们可以使用 problem.options 命令来设置选项。
名称问题可以更改为任何字符或字符串。例如,让我们使用问题结构来找到非线性函数的根。
请参阅下面的代码。
clc
clear
p.objective = @(x)sin(cosh(x));
p.x0 = 1;
p.solver = 'fzero';
p.options = optimset(@fzero);
root = fzero(p)
输出:
root =
1.8115
我们还可以从 fzero() 函数中获取其他信息,例如函数值、指示退出条件的退出标志以及有关寻根过程的信息。
退出标志可以返回 1(表示函数收敛)、-1(表示算法由于输出或绘图函数而终止)、-3(表示无穷大或 NaN 值是遇到)、-4(表示遇到复数)、-5(表示算法收敛到奇异点)和 -6(表示函数未检测到符号的变化)。
例如,让我们找到一个非线性函数的根并获取有关该过程的所有信息。请参阅下面的代码。
clc
clear
Myfun = @(x) exp(-exp(-x)) - x;
x0 = [0 1];
[root fval exitflag output] = fzero(Myfun,x0)
输出:
root =
0.5671
fval =
0
exitflag =
1
output =
struct with fields:
intervaliterations: 0
iterations: 5
funcCount: 7
algorithm: 'bisection, interpolation'
message: 'Zero found in the interval [0, 1]'
该函数还返回迭代之间的间隔、迭代总数以及用于查找非线性函数根的算法。查看此链接了解有关 fzero() 函数的更多详细信息。
