在 Java 中使用递归绘制 Koch 雪花图

本文将解释如何在 Java 中使用递归制作 Koch 雪花。
在 Java 中使用递归绘制 Koch 雪花
科赫曲线也被称为雪花曲线,因为它像雪花一样形成。分形曲线之一就是这个。
下面是具体的绘制方法。
- 将等边三角形的每一边分成三个相等的部分。
- 取中间段的一侧三等分后,删除中间段,以构成等边三角形。
- 重复前两个步骤,画一个较小的三角形。
- 继续直到达到无穷大,产生的曲线就是科赫曲线。
让我们看一个例子。一小簇西兰花可以看作是较大簇的一个分支,在不同的尺度上表现出自相似的形式。
较小的分支可以扩展到适当的比例,以创建一个几乎与整体相同的集群。因此,我们可能会争辩说这样的西兰花簇是分形的。
以下是分形的一些性质:
- 分形集包含任何微小尺寸的精细结构或尺度特征。
- 太不规则了,不能用经典欧几里得几何来表示。
- 自相似豪斯多夫维数将大于拓扑维数,至少是粗略的或任意的。
传统的几何词汇无法解释分形集。它既不是满足特定标准的点的路径,也不是一些基本方程的解集。
自相似性存在于分形集中,无论是近似自相似性还是统计自相似性。在大多数情况下,分形集的分形维数高于其等效的拓扑维数。
一个相对简单的过程在最令人信服的情况下定义了分形集,并且可以将其创建为变换的迭代。
各种图根据不同的绘制技术调用递归实现,如科赫曲线。
研究此代码的算法并将其用作其他 Java 小程序的模型。
递归 Serpienski Gasket 是这个递归 Koch 雪花程序的主要参考,下面的公式用于创建源代码。
源代码:
package KochSnowflakes;
import java.awt.*;
import javax.swing.*;
public class RecursiveKochSnowFlakes extends JApplet {
int initiallevel = 0;
public void init() {
String StringLevel = JOptionPane.showInputDialog("Enter the Recursion Depth");
initiallevel = Integer.parseInt(StringLevel);
}
public void paint(Graphics z) {
DrawKoch(z, initiallevel, 20, 280, 280, 280);
DrawKoch(z, initiallevel, 280, 280, 150, 20);
DrawKoch(z, initiallevel, 150, 20, 20, 280);
}
private void DrawKoch(Graphics z, int level, int a1, int b1, int a5, int b5) {
int delX, delY, a2, b2, a3, b3, a4, b4;
if (lev == 0) {
z.drawLine(a1, b1, x5, y5);
} else {
delX = a5 - a1;
delY = b5 - b1;
a2 = a1 + delX / 3;
b2 = b1 + delY / 3;
a3 = (int) (0.5 * (a1 + a5) + Math.sqrt(3) * (b1 - b5) / 6);
b3 = (int) (0.5 * (b1 + b5) + Math.sqrt(3) * (a5 - a1) / 6);
a4 = a1 + 2 * delX / 3;
b4 = b1 + 2 * delY / 3;
DrawKoch(z, level - 1, a1, b1, a2, b2);
DrawKoch(z, level - 1, a2, b2, a3, b3);
DrawKoch(z, level - 1, a3, b3, a4, b4);
DrawKoch(z, level - 1, a4, b4, a5, b5);
}
}
}
输出:
-
如果我们输入
0作为递归深度,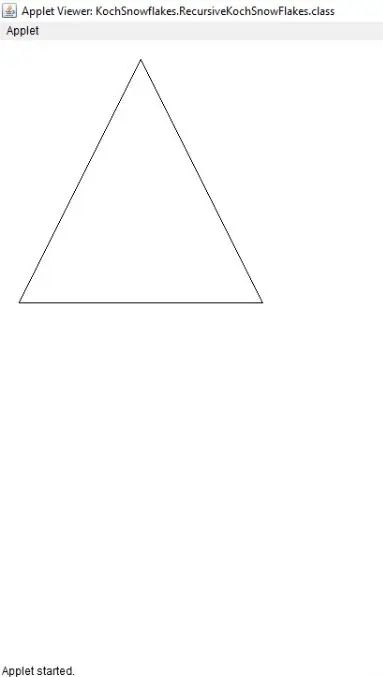
-
如果我们输入
1作为递归深度,
-
如果我们输入
2作为递归深度,
-
如果我们输入
3作为递归深度,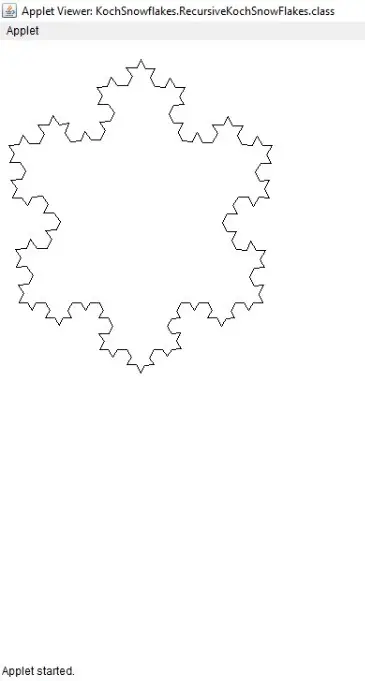
-
如果我们输入
4作为递归深度,
I have been working as a Flutter app developer for a year now. Firebase and SQLite have been crucial in the development of my android apps. I have experience with C#, Windows Form Based C#, C, Java, PHP on WampServer, and HTML/CSS on MYSQL, and I have authored articles on their theory and issue solving. I'm a senior in an undergraduate program for a bachelor's degree in Information Technology.
LinkedIn