Java 中的红黑树
本教程对最著名的数据结构技术之一红黑树进行了最新和深入的检查。此外,我们还针对我们认为你必须理解的基本元素执行了一些 Java 演示程序。
尽管本文结合了红黑树的所有基本特征,但我们的目标是使其尽可能简单。但是,我们也知道初学者理解这个主题可能具有挑战性。
因此,我们推荐阅读:二叉搜索树。
红黑树
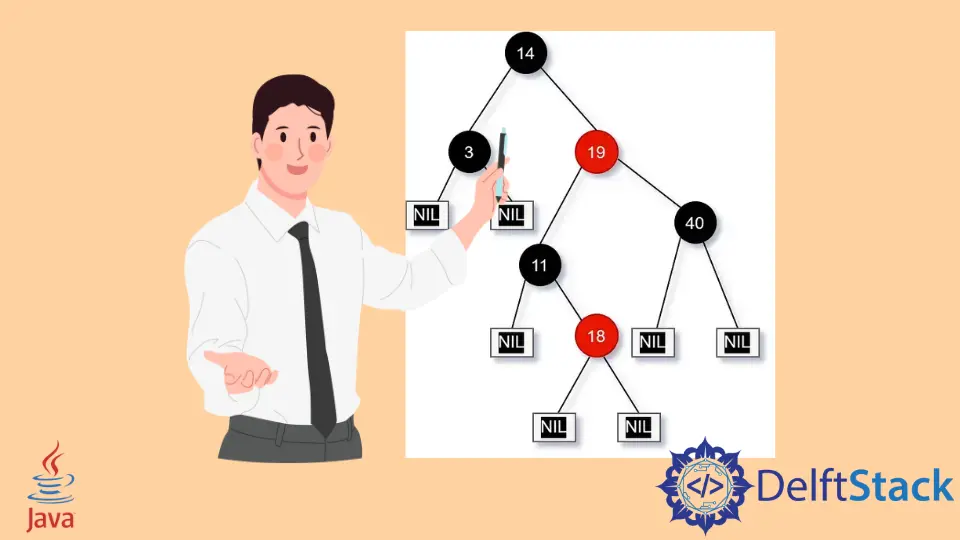
红黑树是计算机科学中独特的二叉搜索树,特别是在数据结构和算法方面。我们使用它来对复杂问题陈述的可比较数据位进行分组。
下表包含有关红黑树的一般信息。
| No. | 树的类型 | 自分支,二叉搜索树 |
|---|---|---|
| 1 | 创造者 | 鲁道夫拜耳 |
| 2 | 函数 | 搜索、插入、检测 |
| 3 | 空间复杂度 | O(n) |
| 4 | 时间复杂度 | O(log n) |
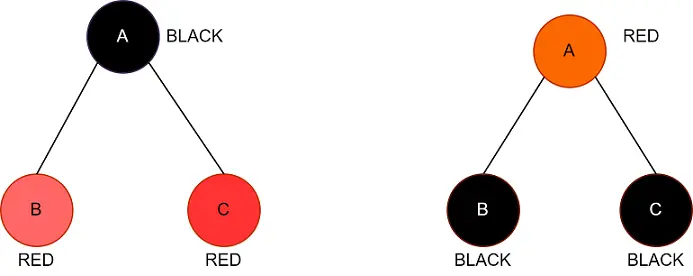
图 1:典型的红黑树(演示示例)。
红黑树的性质
红黑树必须满足以下条件。
- 每个节点都有红色或黑色。
- 我们将
NIL (= NONE)-孩子`` 称为树的叶子。 - 每个
NIL-leaf都是黑色的。 - 树的根也必须是黑色的。
- 假设一个节点是红色的,那么这个节点的两个孩子都必须是黑色的。
- 从节点到后代叶子的所有路径必须包含相同数量的每个节点的黑色节点。
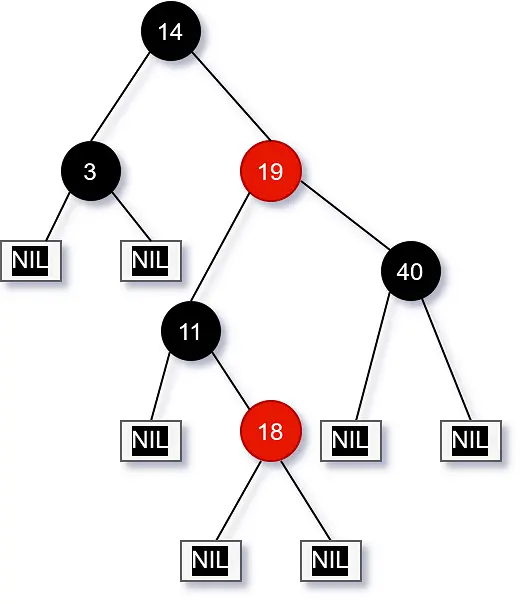
红黑树的高度定义
图 2:树的黑色高度。
树中节点的属性
树节点应包含以下属性。
- 颜色
- 键
- 左孩子
- 右孩子
- 父节点(不包括根节点)
以下是我们稍后将如何处理 Java 程序中的节点。
// class node
public class BlackRedTreeNode {
int Ndata; // The data of the node
BlackRedTreeNode P; // parent
BlackRedTreeNode L; // Left
BlackRedTreeNode R; // Right
int Nclr; // Color of the node
} // end of class
确定红黑树的平衡
我们将假设使用一种数据结构算法的方法来解决如何平衡红黑树结构的问题陈述。
节点颜色限制确保从根到叶的任何简单路径不超过任何其他此类路径的两倍。它增加了红黑树的自平衡能力。
- 节点高度:
Hn T作为树
你可以看到通往叶子的最长路径的边缘。
node-x的黑色高度:
bh(x) 表示黑色节点的数量,包括从 x 到叶子的路径上的 nil [T],但不包括 x。
- 无叶子:
树中的这些属性仅用于计数(属性编号 6)。
-
引理:具有
n个节点的红黑树的高度:
$$
≤ 2 log (n+1)
$$
-
证明:以任意节点
x为根的子树至少包含:
$$
2^bh(x) -1
$$
因此,黑色高度为 bh(x) 的最小子树和完整树具有 n 个内部节点:
$$
2^bh(root[T]) -1 ≤ n
$$
$$ bh(root[T]) ≤ log (n+1) $$ 高度 (T) = 到叶子的最长路径上的边数
$$ ≤ 2 . bh (root[T]) $$
$$ ≤ 2 log (n+1) $$
红黑树中的子树旋转
旋转是为自平衡二叉搜索树设计的独特操作,需要 O(1) 才能完成。此外,相同的旋转有助于保持键的有序遍历。
此外,在旋转操作期间交换子树节点的位置。当其他操作,如插入和删除,违反了红黑树的属性时,会执行旋转操作来恢复它们。
旋转分为两种:
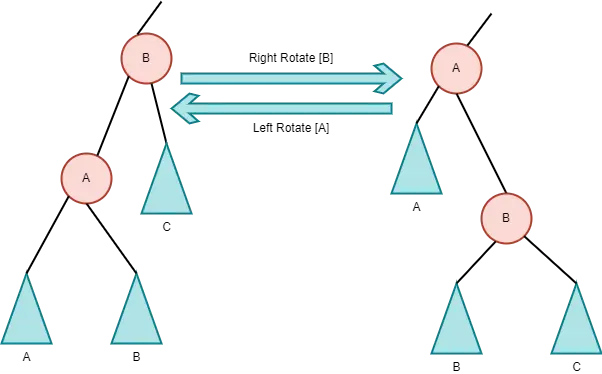
被评估的节点的阿姨会影响进行旋转或颜色更改(当前节点)的选择。如果节点有黑阿姨,我们就轮换。
如果节点有一个红色阿姨,我们反转颜色。我们必须在旋转树后对其进行颜色修复。
在这些操作之后,树应该被终止,如下所示。
右旋转的示例 Java 代码:
// function
// n as node
// P as Parent
// R as Right
// L as Left
// LC as LeftChild
private void RightRotation(TreeNode n) {
TreeNode paPrent = n.P;
TreeNode LC = n.L;
n.L = LC.R;
if (LC.R != null) {
LC.R.P = n;
}
LC.right = n;
n.P = LC;
Replace(P, n, LC);
} // end of function
Java 中的左旋转示例:
// function left rotation
private void LeftRotation(TreeNode n) {
TreeNode P = n.P;
TreeNode Rc = n.R;
n.R = Rc.L;
if (Rc.L != null) {
Rc.left.P = n;
}
Rc.left = n;
n.P = Rc;
replace(P, n, Rc);
} // end of function
搜索算法:红黑树
搜索的工作方式与任何二叉搜索树的工作方式相同。我们首先将搜索键与根进行比较。
如果你的搜索关键字较小,则在左子树中继续搜索;如果搜索关键字更重要,则在右子树中继续搜索。
我们重复这个过程,直到找到我们想要的节点。换句话说,直到我们到达一个零叶点。
假设我们到达一个零叶子,这意味着我们正在寻找的键不在树中。
代码:搜索
// Sn as Search Nodes
// k as Key
// n as node
// r as Right
// d as Data of the data
// L as left
// Function starts here
public TreeNode Sn(int k) {
TreeNode n = r;
// determine the search by applying while loop
// loop starts
while (n != null) {
// checking the key
if (k == n.d) {
return n;
} else if (k < n.d) {
n = n.L;
} else {
n = n.R;
} // condition ends
} // loop ends
return null;
} // Function ends here
插入:红黑树 Java
下面的程序演示了一个函数,我们可以使用它在黑红树中插入节点。尽管就数据结构的观点而言它遵循正确的顺序,但完整的执行将因你的方法而异。
下面的代码对于初学者来说还是足够了,尤其是对于初学者。
代码:插入
// iN as insertion node
// k as key of the tree
// r as root of the node
// R as right node
// L as left node
// d as data
// p as parent
public void iN(int k) {
TreeNode n = r;
TreeNode P = null;
// Swaping the nodes
while (n != null) {
p = n;
if (k < n.d) {
n = n.L;
} else if (k > n.d) {
n = n.R;
} else {
throw new IllegalArgumentException(
"The Binary Search Tree already has a node with this key: " + k);
}
}
// A rough example of how you can apporach insertion of the new node in the tree using BST
TreeNode newN = new TreeNode(k);
newN.clr = red;
if (p == null) {
r = newN;
} else if (k < p.d) {
p.L = newN;
} else {
pt.R = newN;
}
newN.p = p;
// Fixing the tree after the insetion
fixingTreeAfterInsertion(newN);
}
红黑树的应用
在 Java 集合库中,红黑树已用于 TreeSet、TreeMap 和 Hashmap。它也用于 Linux 内核:Completely Fair Scheduler、File、Memory 和 Mapping。
此外,Linux 在 mmap 和 munmap 操作中使用它。此外,它们还用于降低 K-mean 聚类算法的时间复杂度。
此外,MySQL 为表搜索实现了红黑树。我们为什么用它?
红黑树确保 O(log(n)) 的插入和删除时间。它们是稳定的搜索树,因此,它们始终保持对数高度 (n)。
考虑将整数 1,2,3,4,5 放入二叉树中。它将 1 设为根,所有后续元素将向右移动,形成一个有效的链表(并且每个操作都需要 O(n) 时间)。
即使平均时间复杂度相同,如果我们考虑最坏的情况,红黑树在时间复杂度方面超过二叉搜索树。
概括
本教程教你什么是红黑树、控制它的规则以及如何评估这些规则。我们还粗略地演示了如何使用 Java 程序来处理它。
本教程中的一些重要内容:
一、红黑树简介
2. 典型的红黑树:演示示例
3. 树中节点的属性
4. 利用数据结构确定红黑树的平衡
5. 红黑树的子树旋转
6. 右旋转
7. 左旋转
8. 旋转、搜索和插入的演示代码示例
参考
Sarwan Soomro is a freelance software engineer and an expert technical writer who loves writing and coding. He has 5 years of web development and 3 years of professional writing experience, and an MSs in computer science. In addition, he has numerous professional qualifications in the cloud, database, desktop, and online technologies. And has developed multi-technology programming guides for beginners and published many tech articles.
LinkedIn