Java 基数排序算法
Sheeraz Gul
2023年10月12日
在基数排序算法中,元素的排序首先将具有相同位值的单个数字分组,然后按照升序或降序排序。本教程详细解释了基数排序算法,并演示了 Java 中基数排序的实现。
基数排序算法
按照以下步骤应用基数排序。
- 首先从输入数组中找到最大元素;然后,该最大数量将用于遍历所有数组成员的重要位置。
- 接下来,一个一个地走过每个重要的地方。我们可以使用任何稳定的排序算法,例如计数排序,对每个重要位置的元素进行排序。
支持六个元素的数组。radix sort 将首先根据单位位置的值对元素进行排序。
然后根据第十位的值对数组的元素进行排序。
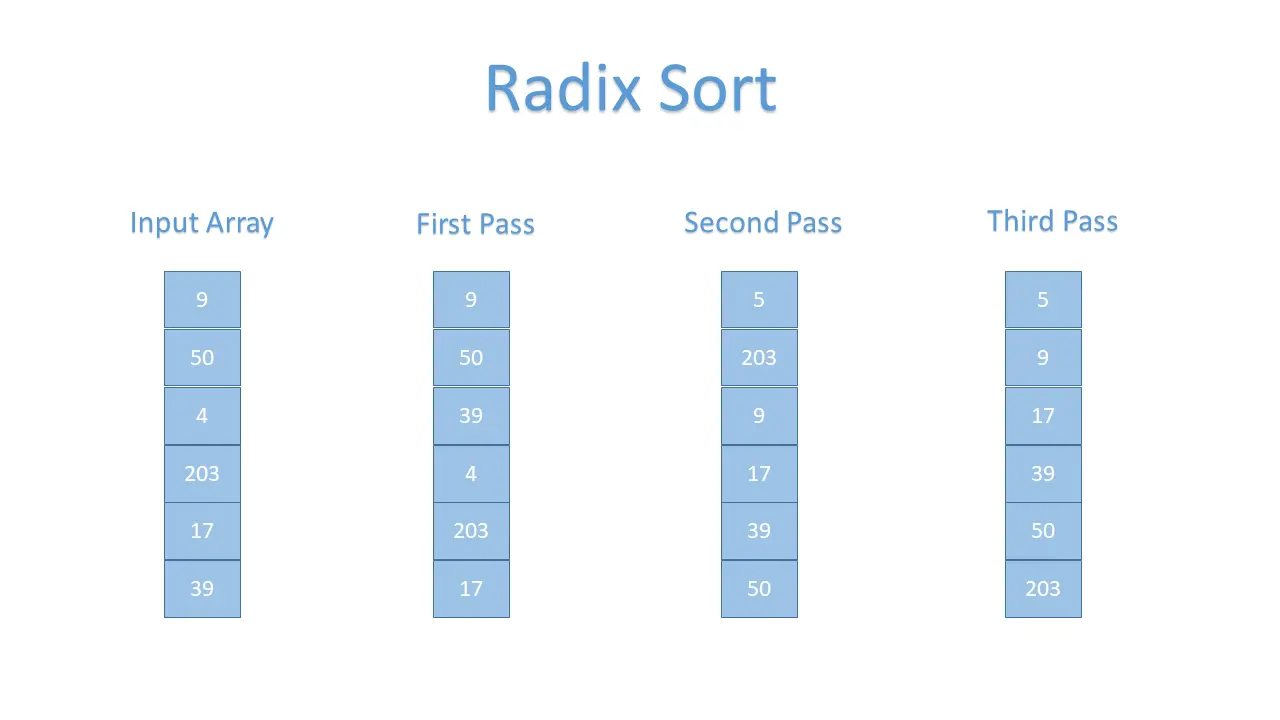
假设数组是 [9, 50, 4, 203, 17, 39]。下图显示了这个数组根据 radix sort 进行了多次排序。

基数排序算法的时间复杂度
下表显示了 radix sort 算法在不同情况下的时间复杂度。
| 时间复杂度 | 情况 |
|---|---|
Ω(n+k) |
最佳情况 |
θ(nk) |
平均情况 |
O(nk) |
最差情况 |
- 最佳情况 - 当不需要排序时,数组已经排序。在最佳情况下,
基数排序时间复杂度是Ω(n+k)。 - 平均情况 - 数组元素的顺序混乱,没有正确的降序或升序。在平均情况下,
基数排序时间复杂度是θ(nk)。 - 最坏情况 - 当数组元素必须以相反的顺序排序时,例如从升序到降序或从降序到升序。在最坏的情况下,
基数排序时间复杂度是O(nk)。
基数排序算法的伪代码
基数排序算法的伪代码如下。
Radix_Sort(Input_Array)
MAX = largest number in the input array
DIGIT = number of digits in the largest number
Now, create DIGIT buckets of size 0 - 9
for x -> 0 to DIGIT
sort the elements according to any stable sort
Java 中的基数排序算法实现
使用计数排序,让我们实现基数排序算法。参见示例:
package delftstack;
import java.util.Arrays;
public class Radix_Sort {
public static void main(String args[]) {
int[] input_array = {9, 50, 4, 203, 17, 39};
int array_size = input_array.length;
Radix_Sort RadixSort = new Radix_Sort();
RadixSort.Radix_Sort(input_array, array_size);
System.out.println("Sorted Array Using Radix Sort: ");
System.out.println(Arrays.toString(input_array));
}
// Counting sort to sort the elements on the basis of significant places
void Counting_Sort(int input_array[], int array_size, int number_place) {
int[] output_array = new int[array_size + 1];
int max_number = input_array[0];
for (int x = 1; x < array_size; x++) {
if (input_array[x] > max_number) {
max_number = input_array[x];
}
}
int[] count_array = new int[max_number + 1];
for (int x = 0; x < max_number; ++x) {
count_array[x] = 0;
}
// Calculating the count of elements
for (int x = 0; x < array_size; x++) {
count_array[(input_array[x] / number_place) % 10]++;
}
// Calculating the cumulative count
for (int x = 1; x < 10; x++) {
count_array[x] += count_array[x - 1];
}
// Sorting the elements
for (int x = array_size - 1; x >= 0; x--) {
output_array[count_array[(input_array[x] / number_place) % 10] - 1] = input_array[x];
count_array[(input_array[x] / number_place) % 10]--;
}
for (int x = 0; x < array_size; x++) {
input_array[x] = output_array[x];
}
}
// Get the largest element from input array
int Get_Max(int input_array[], int array_size) {
int max_number = input_array[0];
for (int i = 1; i < array_size; i++) {
if (input_array[i] > max_number) {
max_number = input_array[i];
}
}
return max_number;
}
// Implement the radix sort
void Radix_Sort(int input_array[], int array_size) {
// Get the maximum number
int max_number = Get_Max(input_array, array_size);
// Apply the counting sort based on significant place value.
for (int number_place = 1; max_number / number_place > 0; number_place *= 10) {
Counting_Sort(input_array, array_size, number_place);
}
}
}
上面的代码在 counting sort 的帮助下实现了基数排序。见输出:
Sorted Array Using Radix Sort:
[4, 9, 17, 39, 50, 203]
作者: Sheeraz Gul
Sheeraz is a Doctorate fellow in Computer Science at Northwestern Polytechnical University, Xian, China. He has 7 years of Software Development experience in AI, Web, Database, and Desktop technologies. He writes tutorials in Java, PHP, Python, GoLang, R, etc., to help beginners learn the field of Computer Science.
LinkedIn Facebook