連結串列反轉
Harshit Jindal
2023年10月12日
連結串列是線性資料結構。連結串列的一個節點包括:
- 資料項。
- 下一個節點的地址。
class Node {
int data;
Node *next;
};
本文將介紹如何在給定指向連結串列頭節點的指標的情況下反轉連結串列。
連結串列反轉演算法
令 head 成為連結列表的第一個節點。
迭代演算法
-
初始化 3 個指標-
curr設定為head,prev和next設定為NULL。 -
遍歷連結列表,直到到達最後一個節點,即
curr!=NULL並執行以下操作:- 將
next設定為curr->next 個,以將next移動到其下一個節點。 - 通過將當前節點指向
prev來反轉其方向。因此,將curr->next設定為prev。 - 將
prev設定為curr,將其向前移動一個位置。 - 將
curr設定為next,將其向前移動一個位置。
- 將
遞迴演算法
-
將列表分為兩部分:第一個節點,即
head節點,以及其餘的連結列表。 -
呼叫
reverse(head->next),即,反向連結列表的其餘部分,並將反向連結列表儲存為rev。 -
將
head附加到反向連結列表rev的末尾。 -
指向
head,即反向連結列表的尾部指向NULL。
使用堆疊的反向連結列表
-
初始化指向連結列表的
head的指標curr。 -
遍歷連結串列,並將每個節點一一插入。
-
將
head更新到連結串列中的最後一個節點,即堆疊中的第一個節點。 -
開始一個接一個地從堆疊中彈出節點,並將其附加到反向連結串列的末尾。
-
將最後一個節點的下一個指標更新為
NULL。
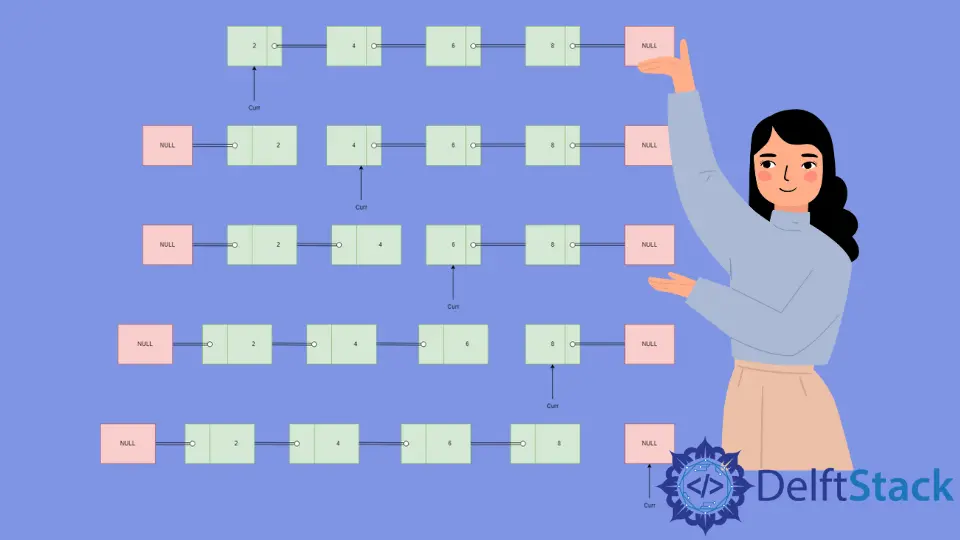
連結串列反轉圖解
-
初始化
curr以指向頭部,即節點2和prev以及curr的資料為NULL。 -
將
next指向curr->next,其值等於4。 -
將
curr->next設定為prev,以獲得以2為首的反向連結列表。 -
將
prev移至curr,即資料為2的節點,將curr移至next,即資料為4的節點。 -
將
next指向curr->next,其值等於6。 -
將
curr->next設定為prev,以獲得以2和4為反向節點,以4為首的反向連結串列。 -
將
prev移至curr,即資料為4的節點,將curr移至next,即資料為6的節點。 -
將
next指向curr->next,其值等於8。 -
將
curr->next設定為prev,以獲得以2,4和6為反向節點且以6為首的反向連結串列。 -
將
prev移至curr,即資料為6的節點,將curr移至next,即資料為8的節點。 -
將
next指向curr->next,即NULL。 -
將
curr->next設定為prev,以2,4,6和8作為反向節點,以8作為頭獲得反向連結串列。 -
將
prev移至curr,即資料為8的節點,將curr移至NULL,演算法終止。
連結串列反轉的實現
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node* next;
Node(int x) {
this->data = x;
this->next = NULL;
}
};
void printList(Node* head) {
Node* curr = head;
while (curr != NULL) {
cout << curr->data << " ";
curr = curr->next;
}
}
Node* reverse(Node* head) {
Node* curr = head;
Node *prev = NULL, *next = NULL;
while (curr != NULL) {
next = curr->next;
curr->next = prev;
prev = curr;
curr = next;
}
head = prev;
return head;
}
Node* recursiveReverse(Node* head) {
if (head == NULL || head->next == NULL) return head;
Node* rest = recursiveReverse(head->next);
head->next->next = head;
head->next = NULL;
return rest;
}
void reverseLL(Node** head) {
stack<Node*> s;
Node* temp = *head;
while (temp->next != NULL) {
s.push(temp);
temp = temp->next;
}
*head = temp;
while (!s.empty()) {
temp->next = s.top();
s.pop();
temp = temp->next;
}
temp->next = NULL;
}
int main() {
Node* head = new Node(1);
head->next = new Node(2);
head->next->next = new Node(3);
head->next->next->next = new Node(4);
head->next->next->next->next = new Node(5);
head->next->next->next->next->next = new Node(6);
head = reverse(head);
printList(head);
cout << "\n";
head = recursiveReverse(head);
printList(head);
cout << "\n";
reverseLL(&head);
printList(head);
cout << "\n";
return 0;
}
連結串列反轉演算法複雜度
時間複雜度
- 平均情況
要反轉完整的連結串列,我們必須訪問每個節點,然後將其附加到反轉表。因此,如果一個連結串列具有 n 個節點,則遍歷的平均情況下時間複雜度約為 O(n)。時間複雜度約為 O(n)。
- 最佳情況
最佳情況下的時間複雜度是 O(n)。它與平均情況下的時間複雜度相同。
- 最壞情況
最差的時間複雜度是 O(n)。它與最佳情況下的時間複雜度相同。
空間複雜度
該遍歷演算法的空間複雜度為 O(1),因為除了臨時指標外,不需要額外的空間。
作者: Harshit Jindal
Harshit Jindal has done his Bachelors in Computer Science Engineering(2021) from DTU. He has always been a problem solver and now turned that into his profession. Currently working at M365 Cloud Security team(Torus) on Cloud Security Services and Datacenter Buildout Automation.
LinkedIn

