二叉樹遍歷

1. 二元樹遍歷
2. 二元樹遍歷圖解
3. 二叉樹遍歷演算法
4. 二叉樹遍歷的實現
5. 二叉樹遍歷演算法的複雜度

二叉樹是一種非線性資料結構。它被稱為二叉樹，因為每個節點最多隻有兩個子節點。這些子節點被稱為左子和右子。它也可以解釋為一個不定向圖，其中最上面的節點稱為根。與線性資料結構只能以一種方式遍歷不同，樹可以以不同的方式遍歷。我們可以通過沿著深度或廣度進行探索來遍歷一棵樹。第一種方法叫做深度優先遍歷，第二種方法叫做廣度優先遍歷。在本文中，我們將討論深度優先遍歷。

深度優先遍歷有 3 種-中序遍歷、前序遍歷和後序遍歷。我們將逐一討論它們。

二元樹遍歷

中序遍歷

在這個遍歷中，我們首先訪問左子樹，然後是根，最後是右子樹。每個節點都類似於一個子樹。對於 BST，中序遍歷按升序返回所有的元素

前序遍歷

在這個遍歷中，我們首先訪問根，然後是左邊的子樹，最後是右邊的子樹。每個節點都類似於一個子樹。它通常用於複製，即建立樹的副本。字首遍歷也有助於從表示式樹生成字首表示式。

後序遍歷

在這個遍歷中，我們首先訪問左子樹，然後是右子樹，最後是根。每一個節點都類似於一個子樹。它被用來有效地刪除樹。它還有助於從表示式樹生成字尾表示式。

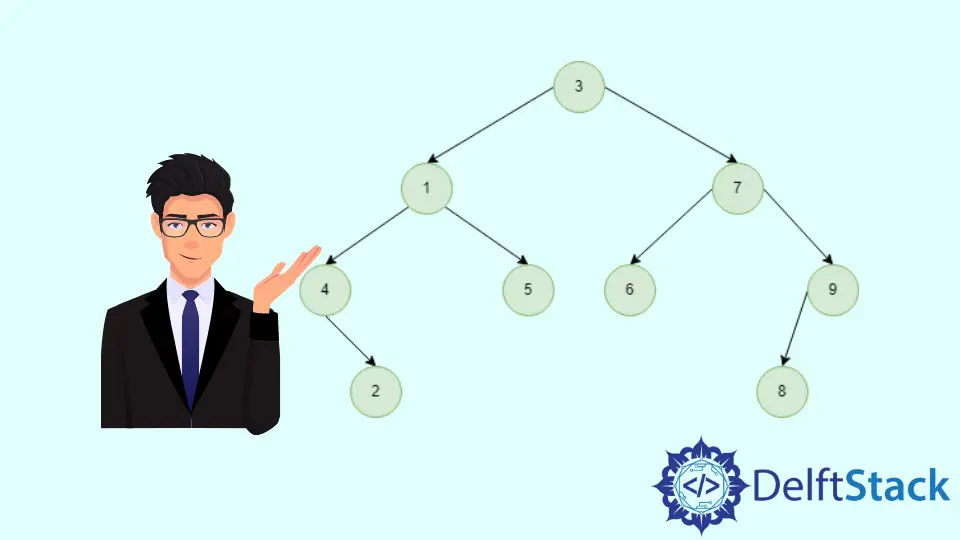
二元樹遍歷圖解

中序遍歷：(4、2、1、5、3、6、7、8、9)

我們在根節點 3 上呼叫中序遍歷。遞迴向左遍歷到達節點 4，它是最左的節點，並將其包含在我們的輸出中；由於它是根節點，沒有左節點，我們訪問它最右的節點 2，並將其包含在我們的遍歷中。這樣，我們遍歷整棵樹，得到上述順序作為我們的輸出。

前序遍歷：(3，1，4，2，5，7，6，9，8)

我們在根節點 3 上呼叫前序遍歷，並將其包含在我們的輸出中。然後我們向左遞迴遍歷到下一個根節點 1，然後是 4。由於 4 沒有左邊的子節點，我們訪問右邊的節點 2。現在我們已經覆蓋了根節點 4 下的子樹，我們回溯到節點 1，並向右走到節點 5。這樣，我們遍歷整棵樹，得到上述順序作為我們的輸出。

後序遍歷：(2，4，5，1，6，8，9，7，3)

我們在根節點 3 上呼叫後序遍歷，向左遞迴遍歷到達節點 4。在將 4 納入我們的遍歷之前，我們必須訪問它的右邊節點 2。1 的右側節點 5 未被訪問，所以我們先將 5 包括在內，然後將 1 輸出。然後我們追溯到根節點 3，並繼續遍歷右邊的子樹。這樣，我們遍歷整棵樹，得到上述順序作為我們的輸出。

二叉樹遍歷演算法

中序遍歷

前序遍歷

後序遍歷

二叉樹遍歷的實現

#include <iostream>
using namespace std;

class Node {
public:
    int key;
    Node *left, *right;
    Node(int x) {
        this->key = x;
        this->left = this->right = NULL;
    }
};

void inorder(Node *root) {
    if (root != NULL)
    {
        inorder(root->left);
        cout << root->key << " ";
        inorder(root->right);
    }
}
void preorder(Node*root) {
    if (root != NULL) {
        cout << root->key << " ";
        preorder(root->left);
        preorder(root->right);
    }
}

void postorder(Node* root) {
    if (root != NULL) {
        postorder(root->left);
        postorder(root->right);
        cout << root->key << " ";
    }
}

int main() {
    Node* root = new Node(3);
    root->left = new Node(1);
    root->right = new Node(7);
    root->left->left = new Node(4);
    root->left->right = new Node(5);
    root->left->left->right = new Node(2);
    root->right->left = new Node(6);
    root->right->right = new Node(9);
    root->right->right->left = new Node(8);
    cout << "The inorder traversal of the tree is : "; inorder(root); cout << endl;
    cout << "The preorder traversal of the tree is : "; preorder(root); cout << endl;
    cout << "The postorder traversal of the tree is : "; postorder(root); cout << endl;
}

二叉樹遍歷演算法的複雜度

時間複雜度

• 平均情況

一棵樹上有 n 個節點，在所有 3 種遍歷中，我們必須去訪問每個節點。由於我們在 n 個節點上迭代，雖然順序不同，但 3 種遍歷的時間複雜度都是 O(n)。平均情況下的時間複雜度是 O(n)。

• 最佳情況

最佳情況下的時間複雜度是 O(n)。它與所有 3 遍歷的平均情況時間複雜度相同。

• 最壞情況

最壞情況下的時間複雜度是 O(n)。它與所有 3 遍歷的最壞情況時間複雜度相同。

空間複雜度

由於遞迴呼叫所需的額外空間，該演算法的空間複雜度為 O(n)。