將二叉樹轉換為二叉搜尋樹
Harshit Jindal
2024年2月15日
二叉樹是一種非線性資料結構。它被稱為二叉樹,因為每個節點最多有兩個子節點。這些子節點被稱為左子和右子。它也可以解釋為一個不定向圖,其中最上面的節點稱為根。二叉搜尋樹(BST)是一種具有特殊屬性的二叉樹,它有助於以排序的方式保持資料的組織。
在本教程中,我們將討論如何將二叉樹轉換為二叉搜尋樹,同時保持二叉樹的原始結構。
將二叉樹轉換為二叉搜尋樹的演算法
-
建立一個名為
arr的陣列來儲存二叉樹節點的順序遍歷。 -
使用任何排序演算法(合併排序 O(nlogn)、快速排序 O(n^2)、插入排序 O(n^2)等)對
arr進行排序。 -
再次對樹進行順序遍歷,並將排序陣列
arr中的元素儲存在二叉樹中,得出 BST。
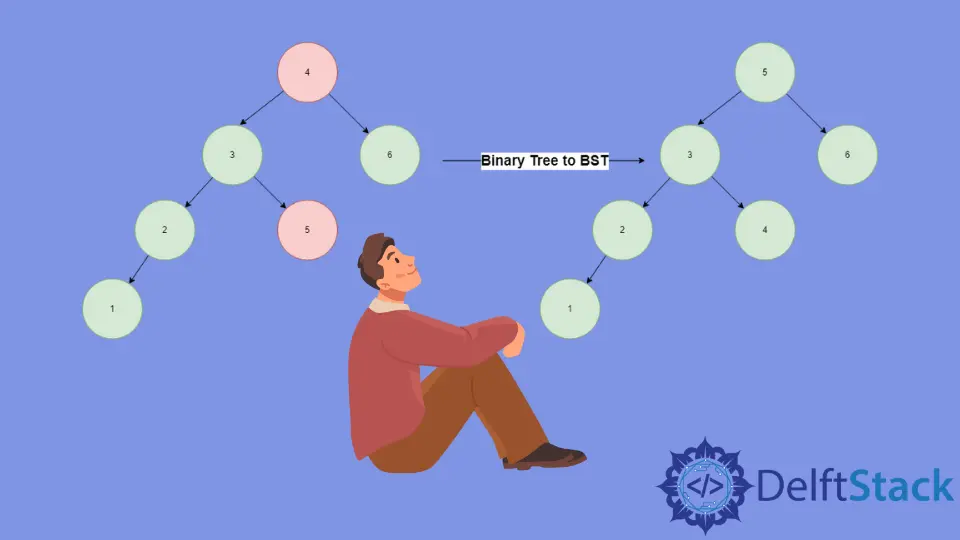
二叉樹轉換為 BST 圖解
-
我們在根節點
4上呼叫順序遍歷。遞迴向左遍歷到達節點1,它是最左的節點,並將其包含在我們的輸出中;由於它是根節點,沒有左節點,我們回溯到節點2,並將其包含在我們的遍歷中。這樣,我們遍歷整棵樹,並將按順序遍歷的結果以[1,2,3,5,4,6]的形式儲存在陣列arr中。 -
使用任意排序演算法對陣列
arr進行排序,得到[1,2,3,4,5,6]。 -
我們再次呼叫順序遍歷,將排序後的陣列
arr儲存回二叉樹中,得到我們的 BST。
二叉樹轉換為二叉搜尋樹的實現
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int data;
Node *left, *right;
Node(int x) {
this->data = x;
this->left = this->right = NULL;
}
};
vector<int> v;
void inorder(Node* root) {
if (root != NULL) {
inorder(root->left);
cout << root->data << " ";
inorder(root->right);
}
}
void storetree(Node* root, int i = 0) {
if (!root) {
return;
}
storetree(root->left);
v.push_back(root->data);
storetree(root->right);
}
void restoretree(Node* root, int& i) {
if (!root) {
return;
}
restoretree(root->left, i);
root->data = v[i];
i++;
restoretree(root->right, i);
}
void converttoBST(Node* root) {
if (!root) {
return;
}
storetree(root);
sort(v.begin(), v.end());
int i = 0;
restoretree(root, i);
}
int main() {
Node* root = new Node(3);
root->left = new Node(1);
root->right = new Node(7);
root->left->left = new Node(4);
root->left->right = new Node(5);
root->left->left->right = new Node(2);
root->right->left = new Node(6);
root->right->right = new Node(9);
root->right->right->left = new Node(8);
cout << "The inorder traversal of the tree is : ";
inorder(root);
cout << endl;
converttoBST(root);
cout << "The inorder traversal of the tree is : ";
inorder(root);
cout << endl;
}
將二叉樹轉換為 BST 演算法的複雜度
時間複雜度
- 平均情況
我們將陣列儲存在 sorted 中,並將 sorted 陣列儲存回二叉樹,進行無序遍歷的時間複雜度為 O(n)。但是,對陣列進行排序的複雜度是 O(nlogn),因此總複雜度給定為 O(nlogn)+2*O(n)。時間複雜度為 O(nlogn)。
- 最佳情況
最佳情況下的時間複雜度為 O(n)。當給定的二叉樹已經是一個 BST 時,我們做無序遍歷來實現它,而且不需要排序操作。
- 最壞情況
最壞情況下的時間複雜度為 O(nlogn)。
空間複雜度
由於遞迴呼叫所需的額外空間,該演算法的空間複雜度為 O(n)。
作者: Harshit Jindal
Harshit Jindal has done his Bachelors in Computer Science Engineering(2021) from DTU. He has always been a problem solver and now turned that into his profession. Currently working at M365 Cloud Security team(Torus) on Cloud Security Services and Datacenter Buildout Automation.
LinkedIn
