二叉搜尋樹迭代插入
Harshit Jindal
2024年2月15日
在上一篇文章二叉搜尋樹中,我們討論了在 BST 中插入節點的遞迴方法。在這篇文章中,我們將討論在 BST 中插入一個節點的迭代方法。它比遞迴方法更好,因為迭代插入演算法不需要額外的空間。
二叉搜尋樹迭代插入演算法
假設 root 是 BST 的根節點,key 是我們要插入的元素。
-
建立要插入的節點-
toinsert。 -
初始化兩個指標,
curr指向root,prev指向 null。(curr遍歷樹,prev保持其蹤跡)。 -
當
curr!=NULL時,執行以下操作。- 更新
prev為curr,以保持其蹤跡。 - 如果
curr->data>key,設定curr為curr->left,丟棄右側子樹。 - 如果
curr->data<key,設定curr為curr->right,丟棄左側子樹。
- 更新
-
如果
prev==NULL,說明樹是空的。建立root節點。 -
否則如果
prev->data>key,則在prev的左邊插入toinsert,prev->left=toinsert。 -
否則如果
prev->data<key,則在prev的右邊插入toinsert,prev->right=toinsert。
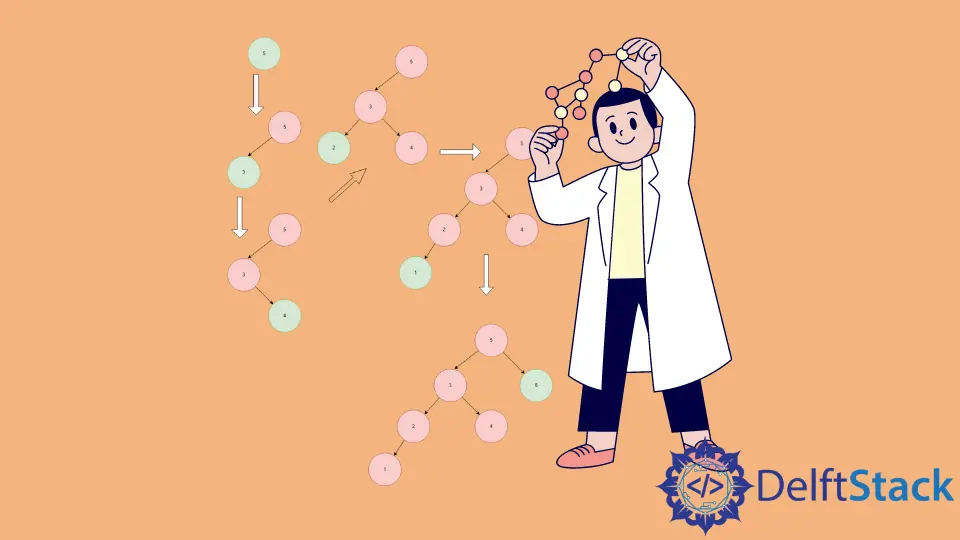
BST 迭代插入圖解
-
首先,我們通過建立一個
root節點來初始化 BST,並在其中插入5。 -
3比5小,所以被插入5的左邊。 -
4比5小,但比3大,所以插入3的右邊,但插入4的左邊。 -
2是當前樹中最小的元素,所以它被插入到最左邊的位置。 -
1是當前樹中最小的元素,所以它被插入到最左邊的位置。 -
6是當前樹中最大的元素,所以它被插入到最右邊的位置。
這就是我們在 BST 內部插入元素的方法。
二叉搜尋樹插入的迭代實現
#include <iostream>
using namespace std;
class Node {
public:
int key;
Node *left, *right;
};
Node *newNode(int item) {
Node *temp = new Node;
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
void inorder(Node *root) {
if (root != NULL) {
inorder(root->left);
cout << root->key << " ";
inorder(root->right);
}
}
void insert(Node *&root, int key) {
Node *toinsert = newNode(key);
Node *curr = root;
Node *prev = NULL;
while (curr != NULL) {
prev = curr;
if (key < curr->key)
curr = curr->left;
else
curr = curr->right;
}
if (prev == NULL) {
prev = toinsert;
root = prev;
}
else if (key < prev->key)
prev->left = toinsert;
else
prev->right = toinsert;
}
int main() {
Node *root = NULL;
insert(root, 5);
insert(root, 3);
insert(root, 8);
insert(root, 6);
insert(root, 4);
insert(root, 2);
insert(root, 1);
insert(root, 7);
inorder(root);
}
二叉搜尋樹插入迭代演算法的複雜度
時間複雜度
- 平均情況
在平均情況下,在 BST 中插入一個節點的時間複雜度與二叉搜尋樹的高度相當。平均來說,一個 BST 的高度是 O(logn)。當形成的 BST 是一個平衡的 BST 時,就會出現這種情況。因此,時間複雜度是 [Big Theta]:O(logn)。
- 最佳情況
最好的情況是,該樹是一個平衡的 BST。最佳情況下,插入的時間複雜度為 O(logn)。它與平均情況下的時間複雜度相同。
- 最壞情況
在最壞的情況下,我們可能要從根節點遍歷到最深的葉子節點,即樹的整個高度 h。如果樹是不平衡的,即它是傾斜的,樹的高度可能會變成 n,因此插入和搜尋操作的最壞情況下的時間複雜度是 O(n)。
空間複雜度
迭代插入操作的空間複雜度為 O(1),因為不需要額外的空間。
作者: Harshit Jindal
Harshit Jindal has done his Bachelors in Computer Science Engineering(2021) from DTU. He has always been a problem solver and now turned that into his profession. Currently working at M365 Cloud Security team(Torus) on Cloud Security Services and Datacenter Buildout Automation.
LinkedIn
