二叉搜尋樹

1. 二叉搜尋樹的搜尋操作
2. 二叉搜尋樹搜尋演算法
3. 二叉搜尋樹搜尋說明
4. 二叉搜尋樹中插入元素
5. BST 插入演算法
6. BST 插入說明
7. BST 搜尋和插入的實現
8. BST 插入和搜尋演算法的複雜度

二叉搜尋樹(BST)是一種基於節點的有序二叉樹資料結構，節點有一個值和兩個子節點(一個二叉樹最多有兩個子節點)左右相連。節點有一個值和兩個子節點(一棵二叉樹最多兩個子節點)左右相連。除根節點外，所有節點只能由其父節點引用。一個 BST 具有以下屬性。

• 左邊子樹上的所有節點都比根節點小。
• 右側子樹中的所有節點都比根節點大。
• 左子樹和右子樹也必須是二叉搜尋樹。

左邊的樹滿足 BST 的所有屬性。另一方面，右側的樹似乎是一個 BST，因為左側子樹的所有節點都較小，而右側子樹的節點較大。但左邊子樹上的節點 1 不符合 BST 屬性，因為它比節點 4 小，但不比根節點 3 大。因此，它不是一個 BST。

由於它是一個有序的資料結構，所以輸入的元素總是以排序的方式組織的。我們可以使用順序內遍歷來檢索儲存在 BST 中的資料，以排序的方式。它之所以得名是因為，就像二叉搜尋一樣，它可以用來搜尋 O(logn) 中的資料。

二叉搜尋樹的搜尋操作

我們知道，在 BST 中，根部右側的元素都比較大，因此如果我們要搜尋的目標元素比根部小，那麼整個右側子樹可以忽略。同理，如果元素比根大，那麼左邊的子樹也可以忽略。我們以類似的方式移動，直到用盡樹或找到目標元素作為子樹的根。如果 BST 是平衡的（如果對於所有節點來說，左子樹和右子樹的高度之差小於等於 1，則稱為平衡樹），那麼 BST 內部的搜尋執行類似於二叉搜尋，因為兩個子樹都有大約一半的元素，在每次迭代時都會被忽略，但如果是一棵不平衡的樹，所有的節點可能存在於同一側，搜尋可能執行類似於線性搜尋。

二叉搜尋樹搜尋演算法

假設 root 是 BST 的根節點，X 是被搜尋的目標元素。

二叉搜尋樹搜尋說明

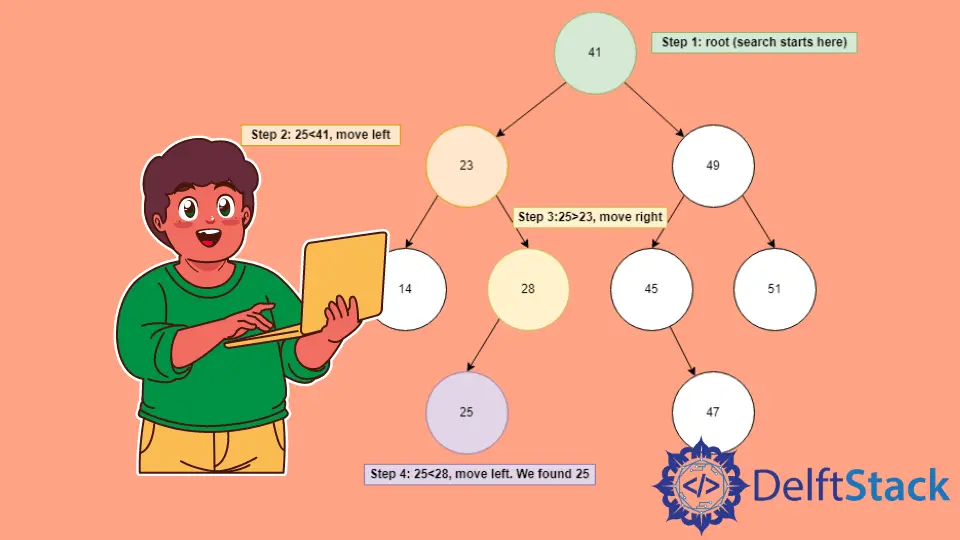
假設我們有上面的 BST，我們想找到元素 X=25。

二叉搜尋樹中插入元素

在 BST 中插入元素的演算法與在 BST 中搜尋元素的演算法非常相似，因為在插入元素之前，我們必須找到它的正確位置，插入和搜尋功能的唯一區別是，在搜尋的情況下，我們返回包含目標值的節點，而在插入的情況下，我們在節點的適當位置建立新節點。

BST 插入演算法

假設 root 是 BST 的根節點，X 是我們要插入的元素。

BST 插入說明

這就是我們在 BST 中插入元素的方法。

BST 搜尋和插入的實現

#include <iostream>
using namespace std;

class Node {
public:
    int key;
    Node *left, *right;
};

Node *newNode(int item) {
    Node *temp = (Node *)malloc(sizeof(Node));
    temp->key = item;
    temp->left = temp->right = NULL;
    return temp;
}

void inorder(Node *root) {
    if (root != NULL) {
        inorder(root->left);
        cout << root->key << " ";
        inorder(root->right);
    }
}

Node* insert(Node *root, int key) {
    if (root == NULL)
        return newNode(key);
    if (key < root->key)
        root->left = insert(root->left, key);
    else
        root->right = insert(root->right, key);

    return root;
}

Node* search(Node* root, int key)
{
    if (root == NULL || root->key == key)
        return root;

    if (root->key < key)
        return search(root->right, key);

    return search(root->left, key);
}
int main() {
    Node *root = NULL;
    root = insert(root, 5);
    root = insert(root, 3);
    root = insert(root, 8);
    root = insert(root, 6);
    root = insert(root, 4);
    root = insert(root, 2);
    root = insert(root, 1);
    root = insert(root, 7);
    cout << search(root, 5)->key << endl;
}

BST 插入和搜尋演算法的複雜度

時間複雜度

• 平均情況

平均而言，在 BST 中插入一個節點或搜尋一個元素的時間複雜度與二元搜尋樹的高度相當。平均來說，一個 BST 的高度是 O(logn)。當形成的 BST 是一個平衡的 BST 時，就會出現這種情況。因此，時間複雜度是 [Big Theta]：O(logn)。

• 最佳情況

最好的情況是，該樹是一個平衡的 BST。插入和搜尋的最佳情況時間複雜度為 O(logn)。它與平均情況下的時間複雜度相同。

• 最壞情況

在最壞的情況下，我們可能要從根節點遍歷到最深的葉子節點，即樹的整個高度 h。如果樹是不平衡的，即它是傾斜的，樹的高度可能會變成 n，因此插入和搜尋操作的最壞情況下的時間複雜度是 O(n)。

空間複雜度

由於遞迴呼叫所需的空間，插入和搜尋操作的空間複雜度都是 O(n)。