R 中的分段迴歸
Sheeraz Gul
2024年2月15日
當資料中有明確的斷點時,使用分段迴歸。本教程演示如何在 R 中執行分段迴歸。
R 中的分段迴歸
當資料中有明確的斷點時,將起作用的迴歸將是分段迴歸。分段迴歸是一步一步的過程,如下所示:
-
建立資料框。
-
擬合資料的線性迴歸模型。我們可以使用
lm()方法來做到這一點。 -
擬合分段迴歸模型。
segmented()方法從segmented包中用於擬合分段迴歸模型。 -
使用
plot()方法視覺化最終的分段迴歸模型。
現在讓我們嘗試使用上述步驟的示例。參見示例:
#Step 1
#create the DataFrame
data<-read.table(text="
Year Stopped
2015 973
2016 1025
2017 1151
2018 1384
2019 4507
2020 15557
", header=T, sep="")
#first six rows of the data frame
head(data)
#Step2
#fit the simple linear regression model
dput(names(data))
q.lm <- lm(log(Stopped) ~ Year, data)
summary(q.lm)
#Step3
#fit the piecewise regression model to original model,
#estimating a breakpoint at x=14
install.packages('segmented')
library(segmented)
o <- segmented(q.lm, seg.Z = ~Year, psi = 2018)
# view the summary
summary(o)
#Step4
# visulize the piecewise regression model
plot(o)
points(log(Stopped) ~ Year, data)
上面的程式碼為在不同年份停止學習的人建立了一個分段迴歸模型。該程式碼有一些輸出,如下所述:
第 1 步的輸出:
Year Stopped
1 2015 973
2 2016 1025
3 2017 1151
4 2018 1384
5 2019 4507
6 2020 15557
它顯示了資料的頭部。
第 2 步的輸出:
Call:
lm(formula = log(Stopped) ~ Year, data = data)
Residuals:
1 2 3 4 5 6
0.50759 0.03146 -0.38079 -0.72463 -0.07216 0.63853
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1057.9257 279.3081 -3.788 0.0193 *
Year 0.5282 0.1384 3.815 0.0189 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.5791 on 4 degrees of freedom
Multiple R-squared: 0.7844, Adjusted R-squared: 0.7305
F-statistic: 14.56 on 1 and 4 DF, p-value: 0.01886
這顯示了線性迴歸模型的摘要。
第 3 步的輸出:
***Regression Model with Segmented Relationship(s)***
Call:
segmented.lm(obj = q.lm, seg.Z = ~Year, psi = 2018)
Estimated Break-Point(s):
Est. St.Err
psi1.Year 2017.91 0.039
Meaningful coefficients of the linear terms:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -162.39260 35.56716 -4.566 0.0448 *
Year 0.08400 0.01764 4.761 0.0414 *
U1.Year 1.12577 0.02495 45.121 NA
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.02495 on 2 degrees of freedom
Multiple R-Squared: 0.9998, Adjusted R-squared: 0.9995
Boot restarting based on 6 samples. Last fit:
Convergence attained in 1 iterations (rel. change 3.7909e-16)
這適合分段迴歸模型並顯示模型的摘要。該模型在 2017.91 年檢測到一個斷點。
第 4 步的輸出:
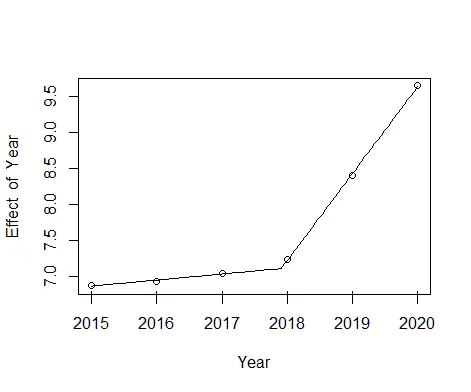
它視覺化分段迴歸模型。該圖顯示分段迴歸模型非常適合給定資料。
作者: Sheeraz Gul
Sheeraz is a Doctorate fellow in Computer Science at Northwestern Polytechnical University, Xian, China. He has 7 years of Software Development experience in AI, Web, Database, and Desktop technologies. He writes tutorials in Java, PHP, Python, GoLang, R, etc., to help beginners learn the field of Computer Science.
LinkedIn Facebook