在 Base R 中執行 K-Means 聚類
本文展示瞭如何在 R 中執行 K-means 聚類。包括視覺化在內的所有步驟都使用基本 R 函式進行了演示。
關於 R 中的 K-Means 聚類
K-means 聚類是一種無監督統計技術,可將資料集劃分為不相交的同質子組。
在進行 K-means 聚類時,我們必須牢記以下幾點。
- 所有變數都必須是數字,因為方法取決於計算方法和距離。用數字編碼的因子資料不是數字。
- 我們的資料集中應該沒有因變數。
- 該方法將每個觀測值分配給一個叢集。因此,它對異常值和資料變化很敏感。
- 它適用於不相交的叢集,但在資料具有重疊叢集的情況下效果不佳。
R 中的 kmeans() 函式
Base R 包含用於 K-means 聚類的 kmeans() 函式。
我們將使用以下引數。
- 第一個引數是資料。
- 第二個引數,
centers,是叢集的數量。 - 第三個引數,
nstart,是用不同的初始質心重複聚類的次數。
K-means 演算法給出了組內總平方和的區域性最優值。這個區域性最優取決於隨機選擇的初始質心。
因此,nstart 用於重複聚類。該函式返回總數最低的叢集。
R 中的 K-Means 模型
為了建立 K-means 模型,我們將建立一個包含兩個變數和三個叢集的資料框。
示例程式碼:
# Vectors for the data frame.
set.seed(4987)
M1 = rnorm(13)
set.seed(9874)
M2 = rnorm(11) + 3
set.seed(8749)
N1 = runif(13)
set.seed(7498)
N2 = runif(11) -2
set.seed(6237)
M3 = rnorm(14) - 6
set.seed(2376)
N3 = runif(14) + 1
# Data frames.
df1 = data.frame(M1, N1)
colnames(df1) = c("M","N")
df2 = data.frame(M2, N2)
colnames(df2) = c("M","N")
df3 = data.frame(M3,N3)
colnames(df3) = c("M","N")
DF = rbind(df1, df2, df3) # Final data frame.
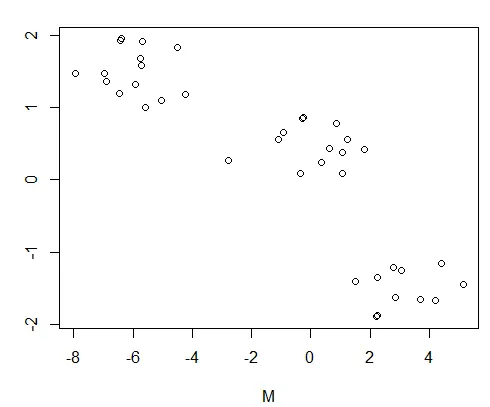
讓我們視覺化這些資料。
示例程式碼:
plot(DF)
資料框圖:
我們現在將建立 K-means 模型。
示例程式碼:
# The K-means model.
set.seed(9944)
km_1 = kmeans(DF, centers=3, nstart = 20)
我們模型中的變數 cluster 儲存了演算法得出的叢集標籤。變數 tot.withinss 儲存組內總平方和。
讓我們看看演算法分配的叢集標籤。唯一重要的是屬於一個叢集的觀察應該具有相同的標籤。
示例程式碼:
km_1$cluster
輸出:
> km_1$cluster
[1] 1 1 1 1 1 1 1 1 1 1 1 1 1 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2
我們發現叢集被正確識別。
簇數 (K)
實際上,我們可能不知道我們的資料有多少簇。在這種情況下,我們需要嘗試不同的 K 值,看看哪個值給出了相當低的組內總平方和。
問題是,隨著 K 的增加,我們將在資料點附近建立更多的質心,並且組內總平方和將下降。
因此,我們需要找到一個相當小的 K 來發現資料中存在的叢集,但不會過度擬合。
通常的方法稱為肘彎法。我們從 1 開始為不同的 K 值建立模型,並繪製每個模型的組內總平方和。
我們在圖中尋找直線斜率變化最大的點。它看起來像手臂的肘關節。為模型選擇了那個特定的 K。
在示例程式碼中,我們將使用一個迴圈來建立模型,並使用一個向量來儲存每個模型的組內總平方和。
示例程式碼:
# Create a vector to hold the total within-group sum of squares of each model.
vec_ss = NULL
# Create a loop that creates K-means models with increasing value of K.
# Add the total within group sum of squares of each model to the vector.
for(k in 1:20){
set.seed(8520)
vec_ss[k] = kmeans(DF, centers=k, nstart=18)$tot.withinss
}
# View the vector with the total sum of squares of the 20 models.
vec_ss
# Plot the values of the vector.
plot(vec_ss, type="l", xaxp=c(0,20,10), xlab="K", ylab="Total within-group-ss")
輸出:
用於估計正確 K 的肘彎圖:
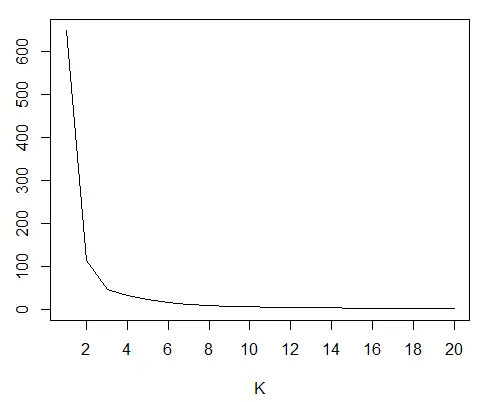
肘部彎曲在 K = 3,這是我們資料的正確值。
在 R 中視覺化叢集
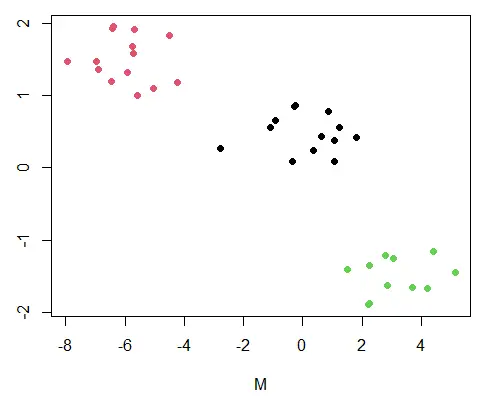
我們可以用散點圖視覺化叢集。顏色引數 col 區分叢集。
簇編號為 1、2、3; col 引數從現有調色盤中為相應的點選擇這些顏色。
示例程式碼:
plot(DF, col=km_1$cluster, pch=19)
輸出:
K 均值聚類圖。
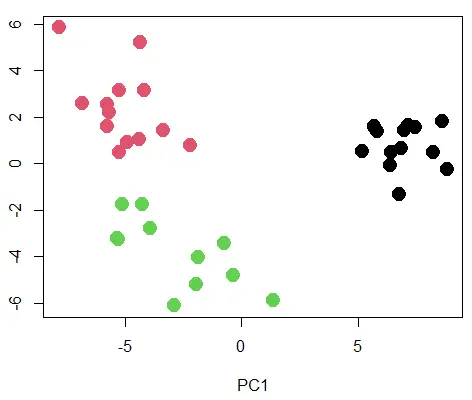
當有兩個以上的變數時,我們可以執行以下操作。
- 建立 K-means 模型並獲得
cluster向量。 - 建立一個主成分模型。
- 繪製前兩個主成分。
示例程式碼:
# First, we will add a third variable to our data frame.
O1 = rnorm(13,10,2)
O2 = rnorm(11, 5,3)
O3 = rnorm(14,0,2)
O = as.data.frame(c(O1,O2,O3))
colnames(O) = "O"
DF = cbind(DF, O)
##################################
# The K-means model.
km_2 = kmeans(DF, centers=3, nstart=20)
# The PCA model.
pca_mod = prcomp(DF)
# Visualize the first two principal components with the cluster labels as color.
plot(pca_mod$x[,1:2], col=km_2$cluster, pch=19, cex=2)
輸出:
帶有聚類的 PCA 散點圖。
其他實際考慮
kmeans()函式使用隨機數生成初始質心。使用set.seed()函式使我們的程式碼可重現。- 我們必須刪除具有缺失值的觀測值才能使用
kmeans()函式。為此,我們可以使用na.omit()函式。 - 我們可以選擇使用
scale()函式縮放每個變數,使其具有0的mean和1的sd。
參考
統計學習簡介一書介紹了使用 R 的 K-means 聚類。
