Python 中的斐波那契數列
Manav Narula
2023年1月30日
- 在 Python 中使用數學公式建立斐波那契數列
-
在 Python 中使用
for迴圈建立斐波那契數列 - 在 Python 中使用遞迴函式建立斐波那契序列
- 在 Python 中使用動態程式設計方法建立斐波那契序列
斐波那契數列是數學中一個常見且經常使用的序列。如下所示。
0,1,1,2,3,5,8,13,21,34,55,89,144,229....
斐波那契數列中的下一個數字是前兩個數字的和,可以用數學方式顯示為 Fn = Fn-1 + Fn-2。
系列的第一個和第二個元素分別是 0 和 1。
在本教程中,我們將討論如何在 Python 中建立這樣的序列。
在 Python 中使用數學公式建立斐波那契數列
斐波那契數列中的每個元素都可以使用以下數學公式表示。
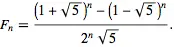
我們可以在 Python 中實現此公式,以找到序列,直到所需的數字,並列印序列。請參考以下的程式碼。
from math import sqrt
def F(n):
return ((1 + sqrt(5)) ** n - (1 - sqrt(5)) ** n) / (2 ** n * sqrt(5))
def Fibonacci(startNumber, endNumber):
n = 0
cur = F(n)
while cur <= endNumber:
if startNumber <= cur:
print(cur)
n += 1
cur = F(n)
Fibonacci(1, 100)
輸出:
1.0
1.0
2.0
3.0000000000000004
5.000000000000001
8.000000000000002
13.000000000000002
21.000000000000004
34.00000000000001
55.000000000000014
89.00000000000003
Fibonacci() 函式用於計算序列中某個位置的斐波那契數。
在 Python 中使用 for 迴圈建立斐波那契數列
我們將使用 for 迴圈建立一個函式以實現所需的序列。在這種方法中,我們將列印所需長度的序列。我們將僅使用 for 迴圈來迭代所需的長度,並在每次迭代時更改所需的變數。下面的程式碼解釋瞭如何操作。
def fibonacci_iter(n):
a = 1
b = 1
if n == 1:
print("0")
elif n == 2:
print("0", "1")
else:
print("0")
print(a)
print(b)
for i in range(n - 3):
total = a + b
b = a
a = total
print(total)
fibonacci_iter(8)
輸出:
0
1
1
2
3
5
8
13
在 Python 中使用遞迴函式建立斐波那契序列
遞迴函式是一個呼叫自身的函式,此類方法可以減少時間複雜度,但使用更多的記憶體。我們可以建立一個函式來返回斐波那契數,並使用 for 迴圈列印所需的序列。
例如,
def rec_fib(n):
if n > 1:
return rec_fib(n - 1) + rec_fib(n - 2)
return n
for i in range(10):
print(rec_fib(i))
輸出:
0
1
1
2
3
5
8
13
21
34
在 Python 中使用動態程式設計方法建立斐波那契序列
動態程式設計是一種將問題分為子問題並儲存這些子問題的值以找到解決方案的方法。此方法通常用於優化問題,可用於生成斐波那契數列,如下所示:
def fibonacci(num):
arr = [0, 1]
if num == 1:
print("0")
elif num == 2:
print("[0,", "1]")
else:
while len(arr) < num:
arr.append(0)
if num == 0 or num == 1:
return 1
else:
arr[0] = 0
arr[1] = 1
for i in range(2, num):
arr[i] = arr[i - 1] + arr[i - 2]
print(arr)
fibonacci(10)
輸出:
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]
請注意,此方法將序列儲存在陣列中。
作者: Manav Narula
Manav is a IT Professional who has a lot of experience as a core developer in many live projects. He is an avid learner who enjoys learning new things and sharing his findings whenever possible.
LinkedIn