在 MATLAB 中繪製斜率場

1. 在 MATLAB 中使用 slope_field() 函式繪製一階普通微分方程的斜率場
2. 在 MATLAB 中使用 quiver() 函式繪製一階普通微分方程的斜場

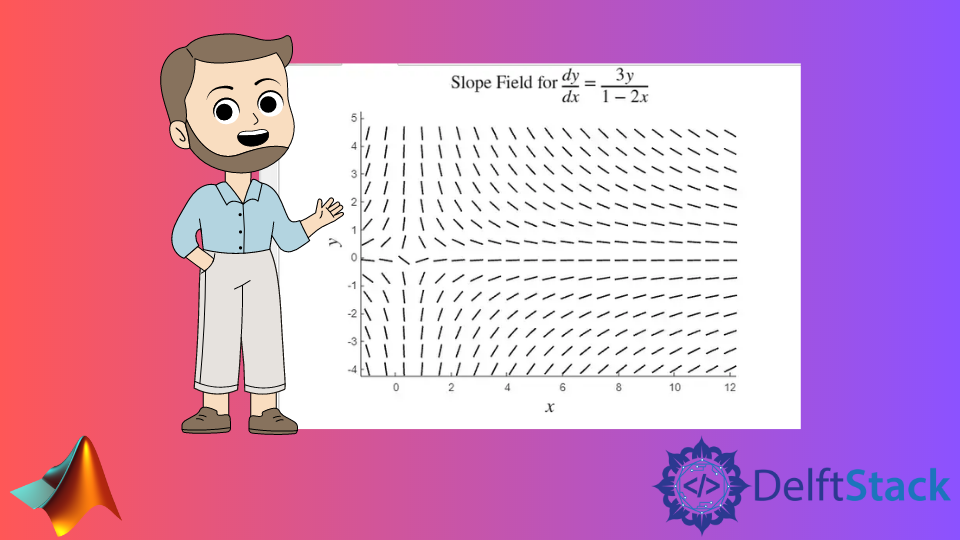
包含函式和相應函式的導數的等式方程構成 (ODE) 常微分方程。

我們使用斜率欄位來闡明我們的微分方程的概念。我們也稱 slope 欄位為 direction 欄位。

在 MATLAB 中使用 slope_field() 函式繪製一階普通微分方程的斜率場

slope_field() 函式包含三個引數。第一個引數是我們正在處理的 f 函式帶有 x 和 y 引數的方程。

第二個引數是我們的 x 引數所在的最小和最大限制。第三個引數是我們的 y 引數所在的最小和最大限制。

這些限制通常稱為 x 和 y 域。函式 slope_field() 幫助我們繪製方程的斜率場，同時返回我們場的圖形控制代碼。

假設，我們的差分方程是：

$$
\frac {dy} {dx} = \frac {3y} {1-2x}
$$

我們將 x 的域設定為 [-1,12]，將 y 設定為 [-4, 5]。

這意味著我們的函式是 f(x,y) = 3y/(1-2x)。

f = @(x,y) 3*y/(1-2*x);
figure;
slope_field(f,[-1,12],[-4,5]);
xlabel('$x$','interpreter','latex','fontsize',17);
ylabel('$y$','interpreter','latex','fontsize',17);
title('Slope Field for $\displaystyle\frac{dy}{dx}=\frac{3y}{1-2x}$',...
    'interpreter','latex','fontsize',17);

輸出：

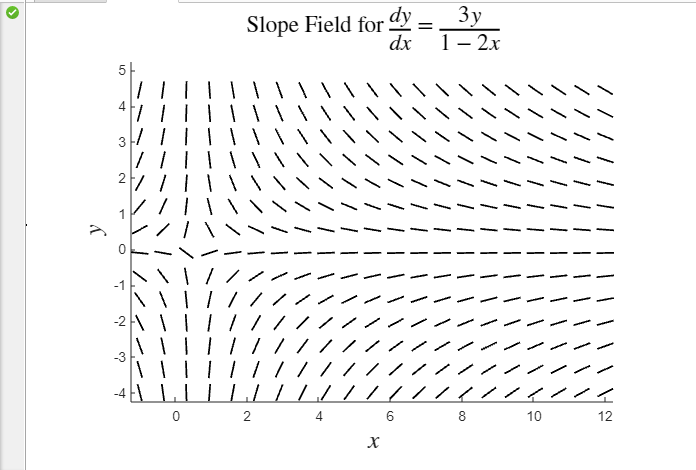
在這個例子中，我們使用了預設設定的 slope_field() 函式，並視覺化了我們想要的微分方程的斜率場。

在 MATLAB 中使用 quiver() 函式繪製一階普通微分方程的斜場

函式 quiver() 包含四個引數：

• X 座標
• Y 座標
• 由 U 表示的 X 座標的方向分量。
• 由 V 表示的 Y 座標的方向分量。

該函式以箭頭形式返回坡度場的圖形表示，其座標為 X 和 Y，方向分量為 U 和 V。

假設，我們的微分方程是：

$$
\frac {dx} {dt} = x^5+6xy-3y
$$

$$
\frac {dy} {dt} = -8x+sin\left(2yx\right)
$$

[x,y] = meshgrid(-3:0.1:3);
dx = x.^5+6*x.*y-3*y;
dy = -8*x+sin(2*x.*y);
r = ( dx.^2 + dy.^2 ).^0.5;
px = dx./r;
py = dy./r;
quiver(x,y,px,py);

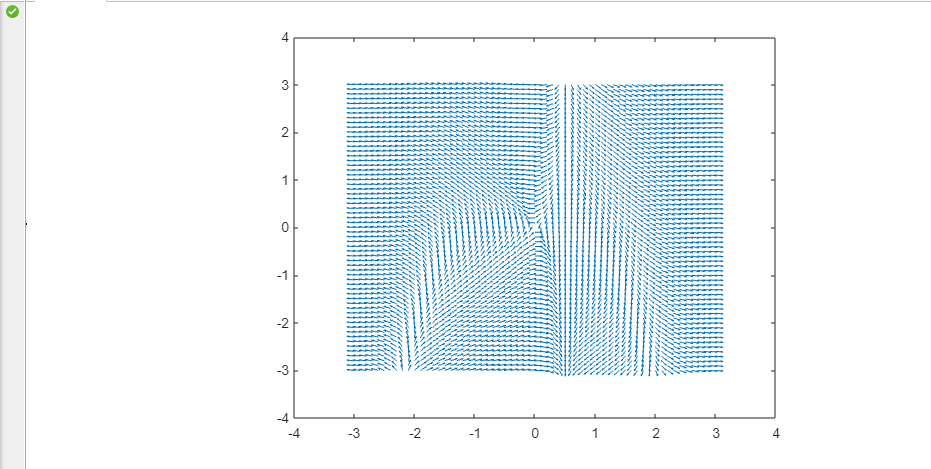
輸出：